Funções Características no Winplot
Esta parte pressupõe familiaridade com o ambiente 2D do Winplot. Vários artigos e tutoriais sobre esse programa podem ser encontrados na seção Laboratórios de Matemática deste site.
Voltemos mais uma vez à função 
da Introdução, cuja definição é
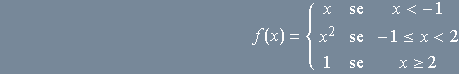
Como produzir o seu gráfico no Winplot? Uma maneira seria usar a função joinx. Na documentação do programa, Richard Parris diz que o gráfico de
joinx(f|c,g|d,...,h)
corresponde ao de
Estritamente falando, essa especificação possui um inconveniente: os extremos direitos c, d, ... dos intervalos são todos fechados 
o que não acontece com a nossa função acima. Na realidade, contudo, o Winplot (como os demais softwares) ignora a diferença entre "
" e
"
" ao produzir o gráfico. Para todos os efeitos, podemos entrar com a expressão
joinx (x|-1,x^2|2,1)
na caixa de funções y=f(x). O resultado é mostrado abaixo:
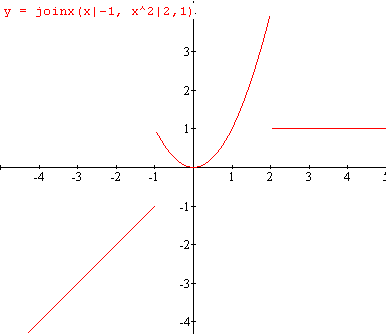
Este é, em essência, o gráfico de 
. Se quisermos usar o recurso de bolas cheias e vazias para chamar a atenção sobre a inclusão ou omissão de extremos de intervalos (como nos livros didáticos), teremos que marcar os pontos 
, 
e 
individualmente, após o que ficaremos com o seguinte:
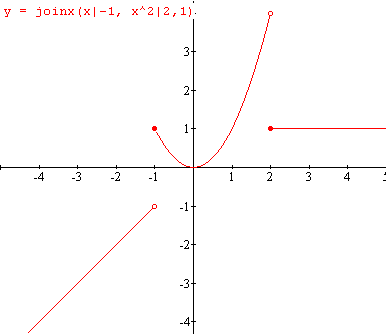
Clique no botão abaixo para ver uma animação na qual o gráfico de
é construído por etapas: os gráficos de 
, 
e 
são sucessivamente traçados e, depois, as partes apropriadas são retiradas passo a passo.
Durante várias exibições que fiz do Winplot, notei que estudantes e professores achavam difícil dominar a sintaxe da função joinx. Em 10 de fevereiro de 2001 enviei um e-mail a Richard Parris no qual sugeria a inclusão de funções características de intervalos no Winplot. Rick se interessou de imediato e, nos dias que se seguiram, discutimos vários detalhes sobre sintaxe e implementação. (Parte da nossa correspondência é mostrada no final deste artigo.) O resultado final foi a inclusão de uma função de três argumentos chamada chi (o equivalente de "qui"
o nome da letra 
em inglês). Em sua documentação, Richard diz que
"chi(a,b,x) = the characteristic function of interval [a,b]"
mas é fácil descobrir que, na verdade, chi(a,b,x) se comporta como a função característica do intervalo semi-aberto 
. Observe que os dois primeiros argumentos são os extremos do intervalo e o terceiro argumento é a variável da função.
De posse da função chi, podemos gerar o mesmo gráfico acima escrevendo
x chi(ninf,-1,x)+x^2 chi(-1,2,x)+chi(2,pinf,x)
na caixa de funções. Como antes, os pontos abertos e fechados têm que ser introduzidos individualmente. Reconhecemos que essa expressão é mais longa do que aquela em termos de joinx, mas, em contrapartida, a sintaxe e a semântica estão mais próximas da prática matemática tradicional. Além disso, os usuários do Winplot têm agora como explorar diretamente as funções características muito antes da universidade!
Clique no botão abaixo para iniciar mais uma animação, na qual se vê o movimento de um ponto sobre o gráfico acima. Observe os saltos do ponto móvel nos extremos direitos (abertos) dos intervalos 
confirmando que, em sua implementação atual, chi(a,b,x) é mesmo a função característica do intervalo
.