Extensão a Conjuntos Quaisquer
Em nossa definição de "função característica de
", supusemos que
era qualquer subconjunto de 
. Entretanto, mesmo com um computador não é possível fazer o gráfico de qualquer função característica. Na prática, os subconjuntos de
que surgem mais freqüentemente são intervalos ou combinações de intervalos.
Por outro lado, a Matemática não lida apenas com conjuntos de números reais. Podemos ter conjuntos de pares ordenados de números reais, de funções, figuras geométricas, matrizes, vetores, etc. As operações básicas que habitualmente fazemos com conjuntos (união, interseção, etc.) não envolvem restrições sobre a natureza dos seus elementos. Do mesmo modo, a definição que demos de 
certamente faz sentido para qualquer conjunto
.
Exemplo 10
Suponha que 
, o produto cartesiano do intervalo fechado 
por si mesmo. Geometricamente, este produto é um quadrado no plano cartesiano. Algebricamente, o plano cartesiano é o conjunto 
de todos os pares ordenados 
tais que 
. Nada nos impede de considerar a função definida em 
e com valores em 
que associa o número 1 aos pontos do quadrado e o número 0 aos pontos fora dele. Isto é, dado um par 
, o valor desta função em 
é 0 ou 1 conforme a regra
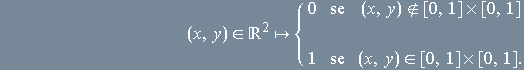
Mas isto nada mais é do que a função característica do conjunto 
. Trata-se de uma função de duas variáveis. Aqueles que possuem conhecimentos de Geometria Analítica Espacial não terão dificuldade em visualizar o gráfico dessa função.
Embora seja natural e fácil lidarmos com funções características de conjuntos quaisquer, são necessários alguns cuidados. A fim de que possamos falar da função característica de um conjunto
, é necessário supor que
é parte de um conjunto 
previamente conhecido. O conjunto será o domínio da função característica. Assim, a função característica de
com relação a um conjunto 
é a função
definida pela mesma regra de antes, isto é,
O que fizemos agora foi realçar o papel do conjunto , o qual atua como um "universo de discurso" ou "conjunto de fundo" numa dada discussão. Quando se diz que "
", subentende-se que isto significa
"
", isto é,
"
". A escolha de
pode variar com o contexto; em diferentes situações, podemos tomar conjuntos universos diferentes para um mesmo 
.
Exemplo 11
Nas páginas anteriores tomamos 
. Quando falávamos em conjuntos, ficava implícito que se tratava de conjuntos de números reais. Por este motivo, as funções características eram todas funções de
em 
.
Exemplo 12
No Exemplo 5, o nosso conjunto de fundo é o plano cartesiano, isto é, o
. Desta vez, os conjuntos de interesse não consistem de números reais, mas de pares ordenados de números reais (subconjuntos do plano). Assim, se 
é um subconjunto do plano cartesiano, então a função característica de 
é a função 
definida como antes: se 
, então 
; se 
, então 
. A definição é formalmente a mesma, exceto que agora "
" não se refere a um número real, mas a um par ordenado de tais números.
Se não mencionássemos um conjunto
como acima, qual poderia ser o domínio da função característica de um conjunto
"arbitrário"? Seria o conjunto de todas as coisas? Acontece que a noção de "conjunto de todas as coisas" 
algo como um conjunto "absolutamente universal", que contém tudo
conduz a paradoxos na Lógica e na Teoria dos Conjuntos (como os paradoxos de Russell e de Cantor). Esses paradoxos são intrigantes e desafiadores, mas felizmente não precisamos nos preocupar com eles na Matemática "comum", onde os conjuntos com os quais lidamos são sempre extraídos de universos bem conhecidos.
Vemos agora que uma função característica fica determinada por um par de conjuntos: um conjunto
e um conjunto
tais que 
. A função característica de
com relação a
é a função de
em 
que é 
em 
e 
fora de
. Deveríamos mencionar os dois conjuntos no nome da função característica de
, mas na prática deixamos
implícito sempre que possível.
As propriedades (1)-(5) que vimos anteriormente são válidas independentemente da natureza dos conjuntos. Entretanto, agora que podemos usar conjuntos mais complicados em estrutura, precisamos alargar a lista de propriedades para incluir novos casos. Damos abaixo um exemplo envolvendo produtos cartesianos. Funções características de uniões, interseções e outras operações aplicadas a coleções de conjuntos não serão discutidas aqui.
Exemplo 13
Como se relaciona a função característica de um produto cartesiano com as funções características dos fatores? Para examinar o caso mais simples, tome dois conjuntos 
. O produto cartesiano 
é um subconjunto de 
. Portanto, a função característica de 
é uma função de
em 
. Assim, dado 
, temos:
Torna-se evidente que
Observe que 
é o produto das funções características de
e 
nas componentes do par 
. Isto é suficiente para a maioria das aplicações.
Clique aqui se você quiser saber como exprimir a própria função característica como um produto de funções.