A Função de Heaviside no Mathematica
Observe que na definição de 
no Exemplo 18, não fizemos uso algum de funções características: a função foi definida usando-se comandos condicionais
como os que se vê em outras linguagens de programação. Contudo, não existem milagres em computação. Sob condições "normais", funções definidas em termos de comandos condicionais clássicos como If, Which ou Switch não são "genuinamente matemáticas". Isto é, elas não respondem a operações como tomar limites, calcular derivadas, integrais, etc. Para se conseguir isto, uma saída consiste em passar esse comportamento para funções características apropriadas e exprimir as funções "genuinamente matemáticas" em termos de funções características (quando possível). Vejamos como isto é feito no Mathematica.
Nas versões mais recentes do Mathematica o kernel contém apenas uma função característica fundamental: é a função de Heaviside, aí chamada de
UnitStep. Após atribuirmos um valor a x (pertencente a 
), a expressão
retornará 
ou 
conforme o valor lógico da condição x>=0 seja verdadeiro ou falso. Em particular, UnitStep[0] é igual a 1. Eis a notação matemática escolhida para a função UnitStep:
Exemplo 19
No Mathematica, ao contrário do que ocorre no Winplot, a fórmula
é válida se e somente se 
. O motivo é que a função sinal no Mathematica assume o valor
em
uma decisão mais natural do que a do Winplot, já que
não tem sinal. Assim, caso se insistisse em manter a fórmula acima para 
, ter-se-ia 
o que, aliás, é comum em muitos livros; veja Butkov[2], p.116. Nas últimas versões do Mathematica, porém, 
.
Exemplo 20
A semântica da função de Heaviside no Mathematica vai muito além de meramente executar um teste tipo If. Um banco de regras de transformação foi associado à função para uso em várias operações, conforme atesta, por exemplo, o cálculo da sua transformada de Laplace
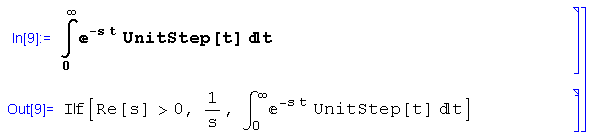
Como já vimos, a função de Heaviside é simplesmente a função característica do intervalo 
. Em teoria, não é necessário dispor de uma função característica para cada tipo de intervalo, já que toda função característica de um intervalo se exprime em termos da função de Heaviside (Exercício 5). Todavia, as transformações envolvidas podem se tornar cansativas em cálculos intensos, além de produzirem expressões longas e pouco intuitivas. Felizmente, o sofisticado sistema de manipulação simbólica do Mathematica nos permite definir funções características de intervalos usando a notação matemática tradicional. Por exemplo, após
carregarmos o pacote para manipulação simbólica
podemos entrar com as notações
A partir daí, o sistema será capaz de interpretar corretamente expressões como 
,
, 
e 
. As definições acima dão conta de intervalos ilimitados; isto é, os extremos podem ser 
ou 
. Isto porque
e
Exemplo 21
Com as definições acima, a função
doExemplo 18 pode ser especificada assim:
Da expressão Plot[f[x],{x,-4,4}] resultará o mesmo gráfico de antes, mas agora é possível aproveitar o banco de regras de UnitStep para o cálculo de limites, derivadas, etc.
Exemplo 22 (continuação)
Eis o cálculo do limite de
à direita de 
(usando TraditionalForm na entrada):
O limite à esquerda é
Como os limites laterais são diferentes, a função é descontínua em
. Obviamente, este fato pode ser facilmente comprovado pelo exame do gráfico de
(que já mostramos no Winplot).
Pode-se fazer muito mais com a função de Heaviside no Mathematica do que mostraremos neste artigo. Por exemplo, a função pode ser usada com mais de uma variável. Aplicações interessantes (envolvendo as funções generalizadas) serão dadas em outra ocasião.