Colando Funções
Uma das utilidades das funções características é que elas nos permitem "colar" funções distintas numa única. Veremos que funções definidas por casos (ou por partes) isto é, por várias fórmulas, podem ser reescritas como uma só se utilizarmos funções características apropriadas. É importante ressaltar que as funções resultantes dessa "colagem" tanto podem ser contínuas como descontínuas.
Exemplo 6
Retomemos a função vista na Introdução, cuja definição é
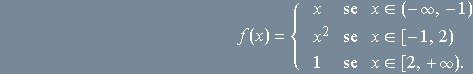
Esta função é definida por três fórmulas distintas. Utilizando as funções características dos três intervalos, podemos encontrar uma expressão única para essa função. De fato,
É fácil entender o mecanismo dessa expressão. O domínio de
é
uma reunião disjunta de três intervalos. Assim, dado um número real 
, temos três possibilidades exaustivas e mutuamente exclusivas: 
ou 
ou 
. Digamos que 
. Então os valores 
e 
são nulos (pois 
não está em nenhum dos dois últimos intervalos), de modo que
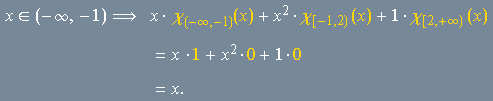
O raciocínio para os demais intervalos é análogo e mostra que a expressão única
é realmente equivalente às três fórmulas que definem .
Exemplo 7
Um exemplo bem conhecido de função definida por partes é a função módulo:
Neste caso, é fácil encontrar fórmulas únicas em termos de expressões algébricas familiares. Por exemplo,
Em termos de funções características, podemos escrever:
O gráfico do módulo é obtido colando-se os gráficos das funções
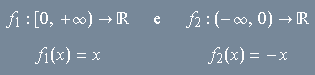
Exemplo 8
Usando a notação do Exercício 2, é fácil ver que
É importante notar que os intervalos acima são 
e 
sem pontos comuns.
Exemplo 9
Analogamente, a função que associa a cada par 
a maior das coordenadas pode ser escrita como combinação de funções características:
