Exemplos
Exemplo 23
Dados 
, com 
, a função semicaracterística do intervalo 
é dada pela expressão
Para ver que assim é, basta notar que
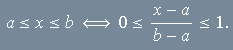
Exemplo 24
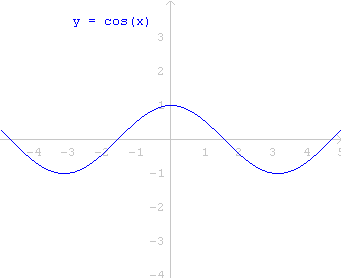
Suponha que você deseja ver o gráfico do cosseno apenas sobre o intervalo 
. Isto é, você deseja ver apenas o pedaço de curva que consiste dos pares
tais que 
e 
. No Winplot, isto pode ser conseguido travando-se os extremos do intervalo de variação de 
na caixa y=f(x).
Sim, mas não queremos usar este recurso. Queremos especificar o pedaço do gráfico por meio de uma condição matemática. Bem, podemos entrar com as equações paramétricas 
com 
. Mas suponha que estamos impedidos de usar equações paramétricas por algum motivo (como numa aula para alunos que nunca ouviram falar de equações paramétricas). Suponha que só temos permissão para usar equações cartesianas. Uma solução seria apresentar o gráfico de
No Winplot, teríamos o seguinte:
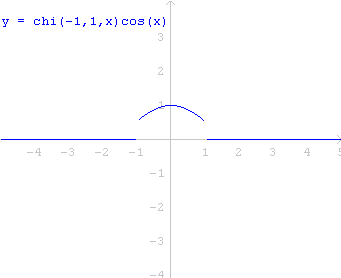
Este gráfico poderia muito bem servir ao propósito, mas há um detalhe irritante: a parte colorida de azul sobre o eixo 
. Isto se deve à presença da função característica do intervalo 
. Fora desse intervalo, 
é zero, de modo que o gráfico cai sobre o eixo 
. Em vez de multiplicar 
pela função característica do intervalo 
, deveríamos multiplicá-la pela função semicaracterística desse intervalo. De acordo com o Exemplo anterior, o ramo que desejamos corresponderia ao gráfico de
Quando 
está fora do intervalo 
, o quociente 
está fora de 
, onde a função one assume o valor "indefinido". É razoável admitir que
Assim, para valores de 
fora de 
, nenhum ponto será marcado e teremos exatamente o ramo desejado.
Exemplo 25 (A helicóide no DPGraph)
Como se pode notar, funções semicaracterísticas são úteis para nos dar pedaços de gráficos de outras funções 
sem produzir "resíduos" indesejáveis. Considere o caso da equação cartesiana
O conjunto das triplas 
que satisfazem essa equação é uma superfície chamada helicóide. A figura abaixo mostra uma helicóide produzida no DPGraph com
É provável que você fique surpreso ao ler que esta superfície é uma helicóide 
supondo que você já a conheça. Cadê aquele atraente formato helicoidal da superfície? Não, isto não pode ser uma helicóide. Clique no botão abaixo para dar uma olhada na "helicóide" que você está acostumado a ver nos livros.
O gráfico que você acaba de ver também foi produzido no DPGraph, só que usando as equações paramétricas (retangulares) da helicóide. Como a helicóide é mais conhecida pelas suas equações paramétricas, esta é a visão que todos temos dessa superfície. Entretanto, essa parametrização gera apenas uma parte "arredondada" da superfície 
o que explica a diferença entre os dois gráficos. Como poderíamos obter o mesmo efeito com as equações cartesianas? Observe: se no gráfico cartesiano tomarmos apenas os pontos 
cujas projeções 
caem sobre um círculo 
, o resultado será o "gráfico paramétrico". Como
fica evidente que o gráfico paramétrico será obtido com
Clique no botão abaixo para ver uma animação que ilustra a idéia. Em todos os quadros dessa animação (feitos no DPGraph), tomamos 
e 
.