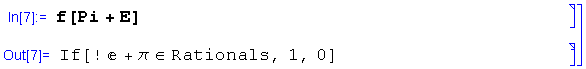Perguntas Sem Resposta
Funções características dos conjuntos numéricos básicos
(onde 
é o conjunto dos números primos) podem ser programadas no Mathematica com base nos símbolos Integers e Rationals. Por exemplo, a função característica do conjunto 
dos números irracionais pode ser definida assim:
O sinal "
" é o símbolo de negação tradicionalmente usado na Lógica. Então, por exemplo,
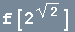
isto é, o número 
é irracional.
Como se sabe (veja o CD Números, Capítulo XVI), a soma de dois números irracionais pode ser ou não irracional. Considere os dois irracionais mais importantes, os números 
e 
. A soma 
é irracional? Perguntemos ao Mathematica:
Como se vê, o sistema basicamente nos devolveu a pergunta. Por quê? Porque ainda não se sabe se o número real 
é irracional ou não! Há muito que os matemáticos demonstraram que 
e 
são irracionais, mas até hoje ninguém conseguiu decidir se 
é irracional. O fato de termos programado a função característica de 
não significa que o computador será capaz de nos devolver um "sim" ou "não" em todos os casos. Para que isto seja possível, é necessário dispor de um algoritmo (um teste finito) que resolva comprovadamente a questão, e depois implementá-lo na máquina. Além disso, o algoritmo tem que ser viável, isto é, eficiente segundo algum critério razoável. Afinal, não ficaríamos contentes em saber que existe um algoritmo capaz de emitir uma resposta após anos de processamento ininterrupto.
A função característica de um conjunto 
é como um oráculo; ela sabe tudo sobre o conjunto. Em princípio, podemos saber se um número real 
está ou não em 
simplesmente calculando 
. Se o resultado for 
, saberemos que
pertence ao conjunto; se for 
, saberemos que não. Acontece que tudo isso funciona apenas em teoria. Na prática, como vimos acima, pode ser extremamente difícil calcular o valor de uma função característica. Quanto é 
? Ninguém sabe.
Funções características são apenas uma maneira conveniente de codificar respostas "sim" ou "não" em termos numéricos. Um problema cuja solução deve ser apenas um "sim" ou um "não" é conhecido na Lógica como um problema de decisão. O estudo de tais problemas pode parecer algo estéril, mas a verdade é que inúmeros problemas matemáticos importantes são ou podem ser reduzidos a problemas de decisão. A relevância de tais problemas torna-se mais evidente quando lidamos com um computador. Se fosse possível resolver todos os problemas numéricos de decisão por meio de algoritmos viáveis, o Mathematica saberia calcular as funções características de todos os subconjuntos de 
. Resultados da Lógica Matemática mostram, contudo, que isto seria verdadeiramente um milagre. Não existem oráculos na Matemática computacional. Existem problemas numéricos de decisão para os quais é impossível elaborar um algoritmo que os resolva. Este é um dos temas "quentes" da Lógica Matemática, sobre o qual nada mais diremos aqui.
O fato de não termos como calcular 
(ou 
) para todo 
tem uma conseqüência interessante: não é possível gerar o gráfico da função 
num computador. Na realidade, um gráfico "perfeito" é impossível por razões mais profundas. Mesmo se o conjunto 
fosse decidível, o gráfico da sua função característica jamais poderia ser exibido fielmente num monitor 
nem mesmo sobre um intervalo limitado (que é o que se pode esperar na prática). O problema aqui é que os números racionais se distribuem pela reta real de maneira extremamente complexa. Conforme mostramos no CD Números (Capítulo XIX), entre dois números reais distintos quaisquer, não importa quão próximos estejam um do outro, existe sempre um irracional. Assim, o gráfico de 
seria algo como a reta 
cheia de "buracos", só que tão próximos entre si que não seria possível discerni-los um dos outros.
Podemos ver agora que, embora a função 
exista como uma entidade matemática para todo
, a sua "realidade" num computador é muito menos palpável, a menos que restrinjamos a natureza do conjunto 
. Conjuntos mais palpáveis e de grande importância prática são os intervalos, cujas funções características podem ser definidas em termos da função de Heaviside. Na página seguinte veremos como esta função se comporta no Mathematica.