A Função de Heaviside
Em sua documentação sobre as funções básicas do Winplot (item Library... do menu Equa), Richard Parris escreve:
hvs(x)=the Heaviside function (1+sgn(x))/2
Aqui, "sgn" se refere à função sinal (signal), cuja definição no Winplot é
sgn(x)=x/abs(x)
Ou seja, o sinal de 
é o quociente de 
por 
; o resultado é simplesmente 
ou 
conforme se tenha 
ou 
, respectivamente. Evidentemente, esta definição de sgn não vale para 
. Contudo, pode-se atribuir valores a "
" de acordo com diferentes convenções. Se marcarmos o ponto 
no Winplot, veremos que 
. Levando este valor na definição de hvs(x) acima, obtemos
A função de Heaviside no Winplot
Mostramos abaixo o gráfico dessa função no Winplot. Para destacar a descontinuidade de salto no ponto 1, "fechamos" o ponto 
e "abrimos" o ponto 
.
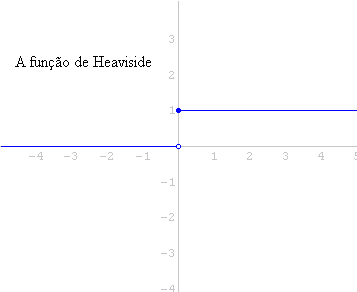
A função de Heaviside é assim chamada em homenagem àquele que a empregou no estudo das equações diferenciais, o engenheiro inglês Oliver Heaviside (1850-1925). Não existe uma notação única para esta função na literatura matemática. Algumas são mostradas abaixo:
Outras notações comuns para a função de Heaviside
Neste site, preferimos indicar a função de Heaviside por 
, de modo que escreveremos
Outra notação para a função de Heaviside
Mencionamos a função de Heaviside aqui porque podemos defini-la em termos de funções características. De fato, é imediato que
Isto mostra que a notação "
" é teoricamente dispensável: a função de Heaviside nada mais é do que a função característica do intervalo 
. Na prática, convenhamos, a notação "
" é mais conveniente.
Outra definição comum em muitos textos é a seguinte:
Mas isto nada mais é do que a função característica do intervalo 
. Com base no Exemplo 5, podemos dizer que
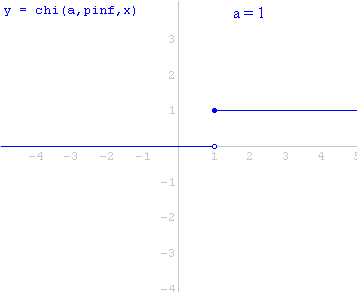
Assim, o gráfico de 
é o gráfico de 
deslocado 
unidades para a direita. Comprove esta afirmação entrando com as expressões
chi(a,pinf,x)
e
chi(0,pinf,x-a)
no Winplot e depois variando o parâmetro 
.
Exemplo 14
Se 
, então
De fato, é suficiente notar que, em virtude das propriedades (1)-(5) já vistas,
Exercício 5
Seja 
um intervalo. Mostre que é possível exprimir 
em termos de 
. Por exemplo, verifique que
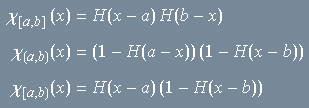
Comprove graficamente esses resultados no Winplot.