Definição e Notação
Seja 
um conjunto qualquer de números reais (isto é, 
). A função característica (em inglês, characteristic function) de
é definida por uma regra extremamente simples. Dado um número real
, ou 
ou 
. Se
, o valor da função em
é 1; do contrário, é 0. A função característica assume apenas esses dois valores: zero ou um. Sua imagem, portanto, é o conjunto 
.
Exemplo 1
A função característica de 
é a função de
em 
que associa a todo número inteiro o valor 1 e a todo número não-inteiro o valor 0. Se chamarmos esta função de 
, então podemos exprimir essa definição dizendo que 
e 
. Mostramos abaixo o gráfico dessa função.
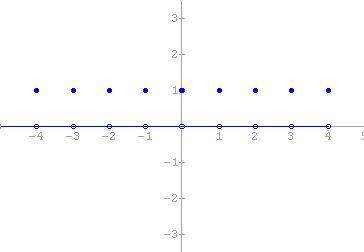
Este gráfico foi feito no Winplot. Para marcar os pontos isolados de uma só vez, crie um ponto em função de um parâmetro e aplique o recurso family. A família de segmentos abertos sobre o eixo x pode ser feita com a mesma técnica.
Observe que a função característica de
depende apenas do conjunto 
. Existe uma notação de uso comum para essa função,
qual seja,
A letra "
" é a vigésima segunda do alfabeto grego e se chama "qui". O "
" é escrito na posição de índice (como em "
"). Assim,
"
" pode ser lido como "qui índice " ou simplesmente "qui ". (Para mais informações sobre o emprego do alfabeto grego na Matemática, consulte o Capítulo II do CD Números.)
Em resumo, o valor de
em 
é o número 
, que é 1 ou 0 conforme se tenha
ou . Alternativamente, podemos dizer que a função
é definida por
Exemplo 2
Voltando ao Exemplo 1, podemos dizer agora que a função característica de 
é 
, dada por
Exemplo 3
Para a função característica do próprio conjunto dos números reais, temos:
Como estamos supondo que o nosso "universo de discurso" nesta página é , a condição "
" é falsa para todo
. Conseqüentemente, vale 
sempre. Ou seja, a função característica de
é a função constante "
", cujo gráfico é a reta paralela ao eixo 
pelo ponto 
.
Exemplo 4
Na definição de função característica de um conjunto
, dissemos que
pode ser qualquer subconjunto de . Logo, podemos tentar 
. O que é a função característica do conjunto vazio? De acordo com a definição,
Ora, como o conjunto vazio não possui elementos, a condição "
" jamais é satisfeita. Resulta que, para todo número real
, 
. Deste modo, a função característica do conjunto vazio é a função constante "
" (ou a função nula), cujo gráfico é (a reta que contém) o eixo das abscissas.