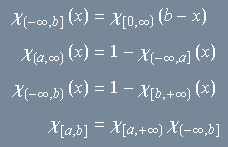Funções Características de Intervalos
Dentre os subconjuntos da reta, os intervalos são especialmente importantes. Na prática, todas as funções que estudamos antes da universidade são definidas em intervalos ou em conjuntos feitos de intervalos. Conforme veremos, algumas funções características de intervalos têm recebido denominações especiais na literatura.
Geometricamente, um intervalo corresponde a um segmento ou a uma semi-reta, com a possível exclusão dos extremos. Podemos deixar que os extremos de um segmento sejam iguais, quando então o segmento se degenera num ponto. Como subconjuntos de
, os intervalos são normalmente
definidos apresentando-se a lista dos seus tipos possíveis. Assim, os intervalos abertos são da forma
onde 
são números reais quaisquer. Portanto, o conjunto vazio é um intervalo, já que
seja qual for 
. Note-se que incluímos a reta inteira na lista dos intervalos abertos.
Os intervalos fechados são conjuntos da forma
Como se pode ver, a reta é um intervalo que é aberto e fechado ao mesmo tempo. O mesmo se aplica ao conjunto vazio, pois podemos dizer, por exemplo, que 
se 
. Note-se ainda que um conjunto unitário 
também é um intervalo, uma vez que 
.
Os intervalos da forma
são limitados; correspondem a segmentos (possivelmente sem um dos os extremos). Já os intervalos do tipo
são todos ilimitados; correspondem a semi-retas (com ou sem extremos). A reta inteira é, obviamente, um intervalo ilimitado.
Toda interseção de intervalos produz um intervalo. Contudo, uma união de intervalos só é um intervalo se eles possuírem um ponto comum. Analogamente, o complemento de um intervalo não é necessariamente um intervalo. De fato, se 
é um intervalo limitado não-vazio, então
não é um intervalo. Por exemplo, o complemento de um intervalo 
, com 
, é
uma união de intervalos que não é um intervalo.
Uma vez entendida as relações fundamentais entre os diversos tipos de intervalo, torna-se fácil manipulá-los em funções características.
Exemplo 5
As afirmações
mostram que
Exercício 4
Verifique os seguintes fatos sobre funções características de intervalos:
