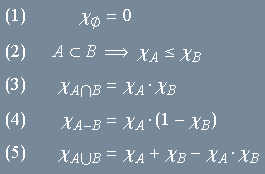Propriedades Fundamentais
As principais propriedades das funções características se encontram abaixo. Elas são válidas para quaisquer conjuntos 
.
Estas afirmações dizem respeito a funções. Cada uma delas é uma maneira econômica de dizer que as relações correspondentes entre os valores das funções são verdadeiras em toda parte. Por exemplo, (1) afirma que a função característica é a função nula, isto é, que
para todo 
. A desigualdade em (2) significa que a desigualdade
é válida para todo 
real. Em (3) estamos dizendo que a função 
é o produto das funções 
e 
, isto é, que a igualdade
é verdadeira para todo . Observações semelhantes valem para os demais casos.
As demonstrações desses fatos são extremamente simples; clique nos links abaixo para ver algumas. Constitui um bom exercício tentar provar coisas desse tipo por si mesmo, sem se basear em indicações prévias.
Prova de (2)
Prova de (3)
A despeito da sua simplicidade, as propriedades (1)-(5) têm muito a dizer em áreas de contato da Lógica com a Álgebra (tabelas de verdade, cálculo proposicional, álgebras booleanas, anéis booleanos, medidas finitas, etc.), mas não discutiremos esses assuntos aqui.
Exercício 1
O
complementar
de um conjunto 
é
o qual denotaremos simplesmente por
Mostre que
Exercício 2
Dados 
, seja 
o menor desses números. Verifique que
Exercício 3
Indique por 
o maior dos números reais 
e 
. Verifique que
