A Função Boole
Voltemos à integral dupla que discutimos na página anterior. Podemos exprimi-la em termos da função característica da região de integração da seguinte maneira:
Este fato é intuitivamente óbvio (supondo-se, claro, familiaridade com os fundamentos da integração), sendo um análogo da propriedade de filtragem do delta de Kronecker (estendido a somas "contínuas"). É natural que se tente implementar este comportamento das funções características numa linguagem de programação com capacidades simbólicas. No caso do Mathematica, isto foi feito por Roger Germundsson com o seu pacote Integration (na pasta Calculus). Após acionarmos o pacote com o comando
a integral acima pode ser calculada como segue:
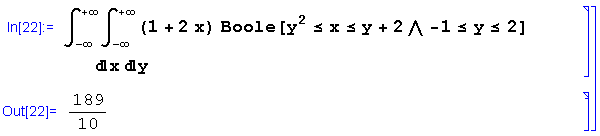
A função Boole, definida no pacote, é uma maneira alternativa de se especificar funções características de conjuntos descritos por sistemas de equações e inequações.
O sinal "
" acima é o símbolo normalmente utilizado na Lógica Matemática para denotar o conectivo "e". Sua presença ali se explica pelo fato de a região
consistir dos pontos 
tais que 
e 
.
Mas a vantagem de se usar a função Boole é que não precisamos descrever
com as inequações típicas de uma região simples. Por exemplo, olhando os gráficos de 
e 
, percebemos claramente que
é a interseção da região côncava da parábola 
com o semiplano 
, isto é,
A função Boole aceita esta descrição:
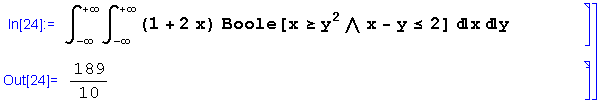
A função Boole é muito mais flexível do que a UnitStep. Em primeiro lugar, todas as funções características de intervalos podem ser definidas facilmente em termos de Boole. Por exemplo,
Em particular,
Em segundo lugar, a função Boole nos permite definir funções características de regiões do plano e de sólidos no espaço tridimensional; basta especificar as inequações apropriadas. Contudo, o uso de Boole sob integrais no Mathematica fica restrito à classe dos conjuntos definidos apenas por inequações polinomiais nas coordenadas cartesianas. Conjuntos definidos por combinações de inequações polinomiais são chamados de semi-algébricos. Estes assuntos serão abordados com mais detalhes em outra seção do nosso site.