Uma Integral Dupla no Mathematica
Nesta página mostraremos como as funções características podem ser úteis na especificação de regiões de integração.
Simmons [5] apresenta como exemplo o seguinte cálculo de uma integral dupla (p. 469, Exemplo 2):
"Calcule 
, onde 
é a região limitada por 
e 
."
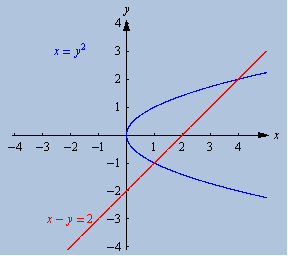
As curvas que limitam a região de integração são mostradas abaixo. Clique sobre a figura para ver a região
.
clique sobre a figura
Lembramos que, para efeitos de integração, as regiões planas mais simples são de dois tipos:
(I) regiões definidas por desigualdades da forma 
, onde
e 
são funções contínuas no intervalo 
.
(II) regiões definidas por desigualdades da forma 
, onde
e
são funções contínuas no intervalo 
.
Tais regiões são sempre limitadas por segmentos horizontais ou por segmentos verticais. Regiões do tipo I, às vezes conhecidas como verticalmente simples, são limitadas verticalmente por gráficos de funções reais de uma variável real. Nas regiões do tipo II, chamadas horizontalmente simples, ocorre o contrário. Como se sabe, integrais de funções contínuas sobre regiões simples se desmembram em duas integrais comuns aninhadas (uma integral de uma integral).
A região
do exemplo de Simmons pode ser vista como sendo do tipo I ou do tipo II.
Vista como uma região do tipo II, é limitada à esquerda pela parábola 
e à direita pela reta 
. Portanto,
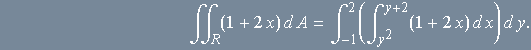
Nesta ordem, o cálculo das integrais é imediato, dando como resultado o número 
. Podemos confirmar isso no Mathematica facilmente:
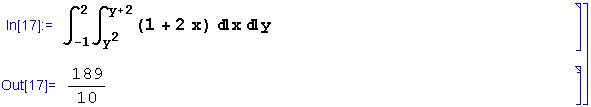
Em sua discussão, Simmons começa tratando
como verticalmente simples (tipo I). Então exprime a integral dupla como soma de duas integrais iteradas e deixa-as apenas indicadas, afirmando que "a outra ordem é mais fácil". De fato é, mas vale a pena examinarmos com o Mathematica onde reside a dificuldade.
A região
é verticalmente simples porque é limitada acima e abaixo por curvas contínuas que são gráficos de funções.
A curva superior é a parte da parábola 
que está acima do eixo 
entre as retas 
e 
. Esta parte é o gráfico de 
restrito ao intervalo 
. Mas surge um pequeno problema com a curva inferior; é claro que se trata do gráfico 
de uma função contínua 
, de modo que
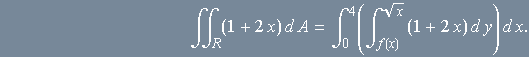
Mas como compactar 
numa expressão única? A solução nos textos tradicionais de Cálculo consiste em evitar essa questão pela observação de que a curva inferior é a justaposição de duas curvas contínuas:
(a) a parte da parábola 
dada por 
para 
;
(b) o segmento da reta 
que liga os pontos 
e 
.
Em cada uma dessas duas partes a curva inferior é dada por uma fórmula única. Assim, decompomos
em duas regiões do tipo I usando essas fórmulas. Como a integral sobre o todo é a soma das integrais sobre as partes, vem
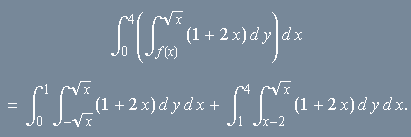
Clique no botão abaixo para ver uma ilustração do processo.
Bem, se você acompanhou este artigo até aqui, certamente perceberá num relance que é possível encontrar uma fórmula única para
em termos de funções características. Temos:
Podemos entrar diretamente com esta expressão na integral dupla? Isto é, podemos calcular
diretamente usando a expressão para
dada há pouco? A resposta é positiva e o cálculo poderia ser feito à mão, conduzindo-nos à mesma decomposição acima. Contudo, estamos interessados em saber como o Mathematica reagirá à definição de
em termos de funções características. Claramente, é muito mais cômodo e elegante exprimir
desse modo e jogá-la numa única integral iterada do que entrar com duas integrais iteradas. Definindo
podemos entrar com
Agora, basta escrever a integral e ver o resultado:
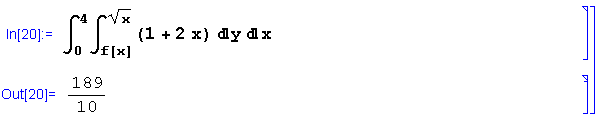
Funcionou!