O Conceito de Rotação No Espaço
Para pontos num plano, uma rotação fica determinada especificando-se um centro, um ângulo e um sentido de giro. No espaço, não falamos de rotação de pontos em torno de um centro (ponto), e sim em torno de uma reta, o eixo de rotação. Mais ainda, o sentido da rotação fica estabelecido orientando-se o eixo e aplicando a “regra da mão direita”: com o polegar apontado para o sentido positivo do eixo, os demais dedos se curvam no sentido da rotação.
É fácil entender a necessidade de se especificar um eixo em vez de um centro quando se discute rotações no espaço. Imagine, por exemplo, como seria a rotação de um ponto 
em torno da origem do sistema 
. É razoável exigir que a distância de
à origem permaneça constante durante a rotação. Assim, o ponto
se movimentará sobre uma esfera de centro na origem. Contudo, isto confere um grau de liberdade à trajetória de
sobre a esfera. Na figura abaixo, feita no Winplot, vemos a trajetória de um ponto
sobre uma esfera de centro na origem.
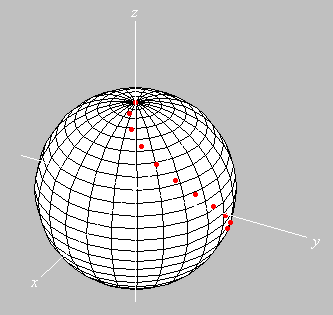
Em cada instante, a distância de
ao ponto 
é constante (igual ao raio da esfera). Todavia, por causa da forma irregular do percurso, não estaríamos dispostos a dizer que
efetuou uma “rotação” em volta de . Para que haja uma rotação, uma condição a mais deve ser satisfeita: o ponto
deve permanecer num plano. A reta que passa pela origem e é perpendicular a esse “plano de rotação” é precisamente o “eixo” em torno do qual se efetua a rotação.
Nas páginas seguintes examinaremos rotações em volta de um dos eixos do sistema ortogonal cartesiano. Rotações em torno de eixos arbitrários serão discutidas em outra ocasião.