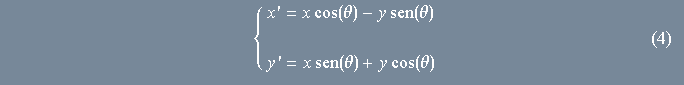O estudo analítico das rotações de figuras geométricas, tanto no plano como no espaço, repousa sobre o seguinte problema:
|
Como se transformam as coordenadas de um ponto no plano após uma rotação segundo um ângulo |
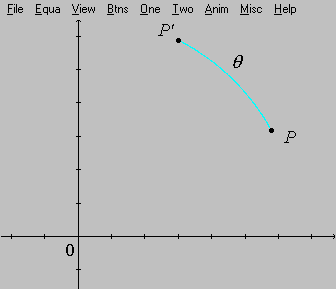
Ou seja, considere um ponto ![]() no plano cartesiano. Imagine agora que o ponto
no plano cartesiano. Imagine agora que o ponto ![]() é girado de um ângulo
é girado de um ângulo ![]() no sentido anti-horário. Após a rotação, cairemos num novo ponto
no sentido anti-horário. Após a rotação, cairemos num novo ponto ![]() . Quais são as coordenadas de
. Quais são as coordenadas de
![]() ? Como se relacionam com as de
? Como se relacionam com as de
![]() ? Existe uma fórmula simples que nos dê as coordenadas
? Existe uma fórmula simples que nos dê as coordenadas ![]() e
e ![]() do ponto
do ponto
![]() em função das coordenadas
em função das coordenadas ![]() e
e ![]() do ponto
do ponto
![]() ?
?
Antes de prosseguir, convém notar um detalhe: não especificamos o centro da rotação. Mencionamos o ângulo (![]() ) e o
sentido (anti-horário) da rotação, mas não o ponto em torno do qual se deve efetuá-la. Quando não dissermos qual é o centro da rotação, ficará implícito que se trata do ponto
) e o
sentido (anti-horário) da rotação, mas não o ponto em torno do qual se deve efetuá-la. Quando não dissermos qual é o centro da rotação, ficará implícito que se trata do ponto ![]() , a origem do sistema ortogonal padrão.
, a origem do sistema ortogonal padrão.
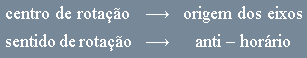
O nosso problema é, portanto, o seguinte: quais serão as coordenadas do ponto
![]() após percorrer um arco de ângulo
após percorrer um arco de ângulo ![]() com centro na origem?
com centro na origem?
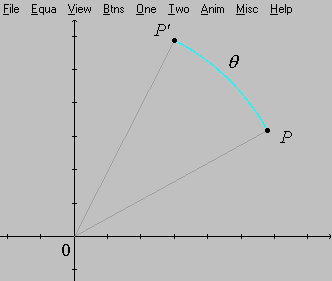
Há várias maneiras de se encontrar uma fórmula para o ponto transformado. Todas elas se baseiam num simples cálculo trigonométrico que estabelece a relação fundamental entre dois sistemas de coordenadas: o retangular e o polar. Entretanto, não é necessário nenhuma familiaridade sistemática com o sistema polar para prosseguir. Sejam ![]() a distância do ponto
a distância do ponto
![]() à origem e
à origem e ![]() o ângulo que o segmento
o ângulo que o segmento ![]() forma com a parte positiva do eixo
forma com a parte positiva do eixo ![]() .
.
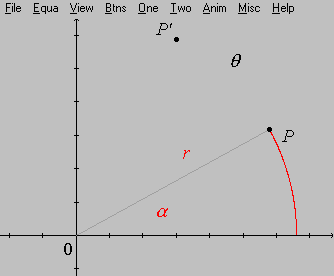
Uma simples figura como esta mostra-nos imediatamente que
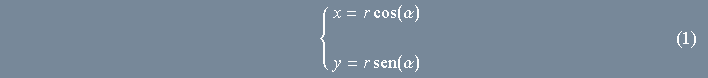
Isso posto, veja o que acontece quando o ponto ![]() gira de um ângulo
gira de um ângulo ![]() : a distância à origem não se altera, mas o ângulo com a parte positiva do eixo
: a distância à origem não se altera, mas o ângulo com a parte positiva do eixo ![]() passa a ser
passa a ser ![]() .
.
Conseqüentemente, para o ponto ![]() obtido após a rotação, teremos
obtido após a rotação, teremos
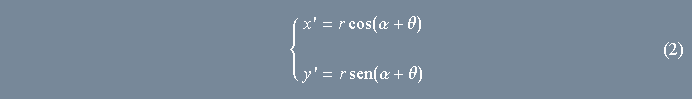
Estamos pertos da solução final. O passo seguinte consiste em desenvolver o cosseno e o seno em (2) de acordo com as bem conhecidas fórmulas para a adição de arcos que aprendemos no colégio. Eis o resultado:
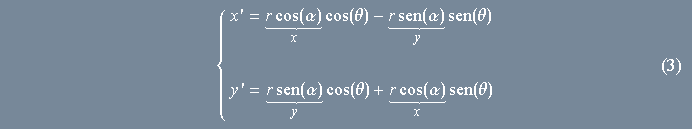
Finalmente, substituímos ![]() por
por ![]() e
e ![]() por
por ![]() em conformidade com as equações (1). Isto nos conduz diretamente a
em conformidade com as equações (1). Isto nos conduz diretamente a

ou ainda, após reordernar os termos de ![]() :
:
equações fundamentais de rotação
Estas são as equações que buscávamos. Elas mostram como as coordenadas de um ponto
![]() se alteram após uma rotação positiva (anti-horária) de ângulo
se alteram após uma rotação positiva (anti-horária) de ângulo ![]() em volta da origem. Mostraremos daqui a pouco como o uso de matrizes facilita
enormemente a memorização dessas fórmulas.
em volta da origem. Mostraremos daqui a pouco como o uso de matrizes facilita
enormemente a memorização dessas fórmulas.