Experiências Matemáticas
Atividade 1
Descubra como alterar as equações paramétricas do toro no Winplot de modo a gerar a superfície gradualmente pela variação de cada parâmetro. (Restrinja cada parâmetro ao intervalo de 0 a 1 e multiplique-o por uma constante dinâmica. Esta técnica foi vista em nosa introdução ao Winplot.)
Atividade 2
Como seria a geração do toro se os parâmetros 
e
variassem simultaneamente sobre o intervalo 
?
Descubra como conseguir esse efeito.
Atividade 3
Aplique as equações de rotação no espaço a (equações de) curvas paramétricas que você conhece e examine os resultados no Winplot. Observe que muitas superfícies comuns são de revolução. Dois exemplos são a esfera e o cone. Você conhece outros?
Atividade 4 (paralelos e meridianos)
Utilize o Winplot para examinar os paralelos e meridianos de uma superfície de revolução dada por suas equações paramétricas. Informalmente falando, os meridianos são as curvas geratrizes. Os paralelos são as interseções da superfície com planos perpendiculares ao eixo de revolução. (Os paralelos são, portanto, as circunferências descritas por cada ponto da geratriz em rotação.) Verifique que essas definições são consistentes com os significados de “paralelo” e “meridiano” no caso familiar da esfera terrestre.
Atividade 5
O Winplot também gera gráficos de superfícies em equações cartesianas. Tais equações são da forma 
. Existe um método simples para se escrever rapidamente a equação cartesiana de uma superfície de revolução em torno dos eixos coordenados a partir da equação cartesiana da curva geratriz. (Numa linguagem como a do
Mathematica, o processo pode ser programado em menos de cinco linhas.) Por exemplo, da equação 
, que define a circunferência de centro 
e raio 1, podemos obter a equação cartesiana do toro que estudamos na seção anterior:
Entre com essa equação no Winplot para ver que ela realmente define o mesmo toro. Entretanto, você verá que o Winplot desenha a superfície de maneira diferente 
pela combinação das curvas de nível nas direções dos eixos.
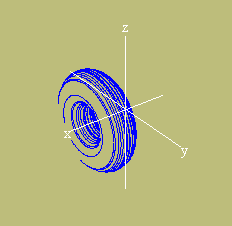
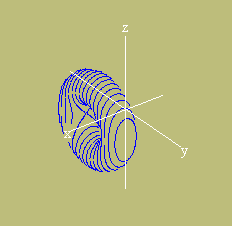
curvas de nível do toro
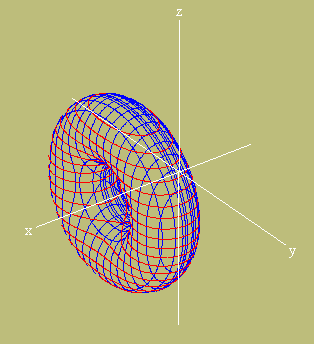
montagem final
Atividade 6
Superfícies de revolução geradas por gráficos de funções 
, tendo retas 
como eixo de revolução, podem ser criadas automaticamente no Winplot; sem a necessidade das equações das superfícies! No ambiente 2D do programa, vá ao item
One e clique em Revolve
surface.... Faça diversos experimentos com curvas que você conhece.
Atividade 7
Nessas lições, discutimos rotações em 
em torno da origem e rotações em 
ao redor dos eixos coordenados. Faça experiências no Winplot e tente descobrir (supondo que você ainda não as conheça) como são as equações de rotação em torno de pontos e eixos (retas) arbitrários. A dedução matemática dessas equações será apresentada numa próxima Lição (na qual discutiremos as translações).
Atividade 8
Crie um cenário no Winplot para explorar o seguinte fato: girar um ponto 
de um ângulo
equivale a mantê-lo fixo e girar os eixos coordenados de 
. Muitos autores preferem apresentar as matrizes de rotação de acordo com esse ponto de vista: em vez de manter os eixos fixos e girar o ponto, o ponto é deixado imóvel e os eixos é que sofrem a rotação. (A linguagem da Álgebra Linear permite uma descrição sucinta e precisa dessas duas interpretações.)