É fácil descobrir quais são as equações de rotação de um ponto em torno dos eixos 
, 
ou 
. Basta mergulhar o plano cartesiano
no espaço cartesiano 
e identificá-lo com o plano de equação 
.
Vistas de , as equações (4) descrevem a rotação de um ponto 
em torno do eixo 
no sentido dado pela regra da mão direita. Assim, se
for o angulo de rotação, o ponto
será levado para o ponto 
tal que
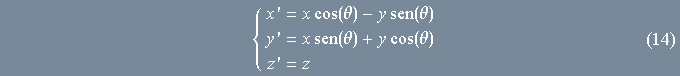
equações fundamentais de rotação em torno de 
A matriz de rotação correspondente (isto é, a matriz dos coeficientes do sistema acima em relação às variáveis 
) é
Um simples raciocínio por analogia nos leva daqui para as matrizes de rotação relativas aos demais eixos coordenados. São elas:
Exemplo 11
Vamos explorar a rotação em torno do eixo
no Winplot. Entre no ambiente 3D do programa e marque o ponto 
.
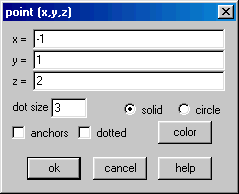
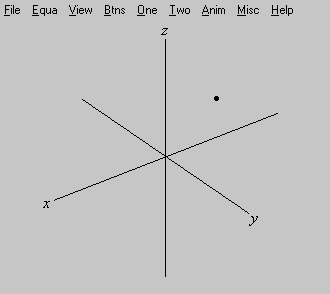
Clique no botão box (caixa) do inventário e defina os limites das coordenadas como abaixo.
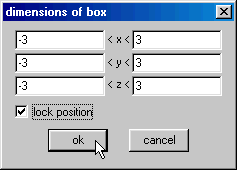
Isto restringe o nosso espaço de trabalho ao cubo 
. Se necessário, acione as teclas de aproximação (zoom in) ou de
afastamento (zoom out). De acordo com a matriz de rotação em torno de
, se o ponto
sofrer uma rotação de ângulo 
em volta desse eixo ele será transformado no ponto
Entre com esse ponto no Winplot.
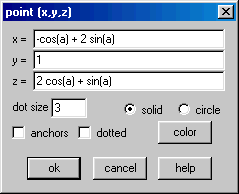
Agora, observe o que acontece quando
varia, digamos, de 
a 
. O ponto
descreve uma trajetória aparentemente circular. Dissemos “aparentemente” por causa dos inevitáveis efeitos de perspectiva.
Como no Exemplo 3, criemos uma família de pontos para melhor visualizarmos a trajetória.
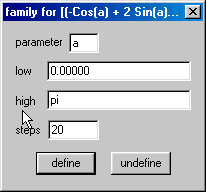
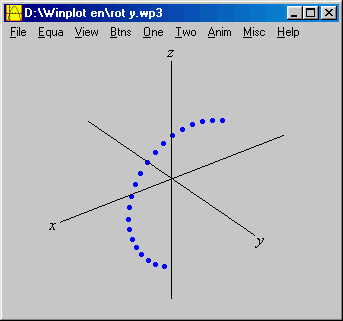
A teoria garante que a trajetória é circular (já que se trata de uma rotação), mas para se convencer visualmente disso talvez seja necessário mudar a nossa posição em relação aos eixos. Usando as quatro teclas de direção na parte inferior do teclado (as setas), podemos movimentar o cenário e nos colocarmos acima do plano 
, como mostram as figuras abaixo.
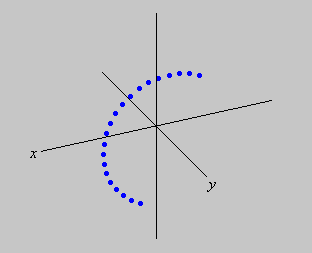
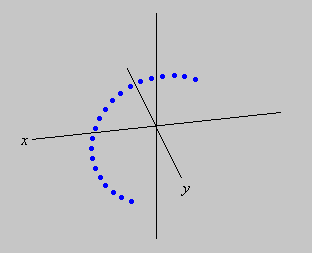
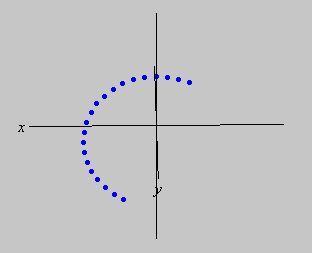
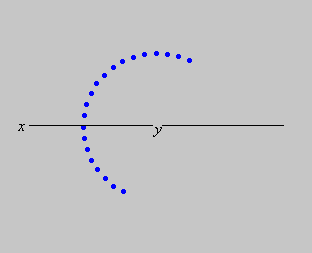
Na última posição, vemos claramente que o ponto efetuou um movimento circular paralelo ao plano
. A teoria está certa! O sentido da rotação coincide com o que é dado pela regra da mão direita: colocando o polegar apontado para a parte positiva do eixo 
, os demais dedos se fecham no sentido da rotação 
que é o sentido do menor ângulo que leva o eixo 
ao encontro de
. Para valores negativos do ângulo, o sentido se inverte.
Esperamos que este exemplo seja suficiente para que você saiba como explorar as rotações de pontos em volta dos eixos coordenados no laboratório fantástico que é o Winplot.