Numa seção anterior, mostramos como as equações de rotação em
nos permitiram girar a parábola 
em volta da origem 
ou ainda, em volta do eixo 
no
. Vejamos como seria girar a parábola no espaço, em volta do eixo 
.
Todas as idéias discutidas a propósito de rotações no
se estendem ao : matrizes de rotação, rotações como transformações, etc. A rotação de ângulo
em torno do eixo 
é a função
dada por
Vista do , a parábola
é o conjunto de todos os pontos da forma 
tais que 
. Para girar a parábola em volta de 
, giramos cada um dos seus pontos. Assim, aplicando a rotação 
à parábola
, os seus pontos serão transformados em
Ou seja, para cada valor de , as equações
parametrizam a curva no
obtida da parábola
por uma rotação positiva de ângulo
em volta do eixo 
.
Exemplo 12
Para visualizar equações paramétricas de curvas no
utilizando o Winplot, clique no item Curve
x=f(t),... do menu Equa do ambiente 3D. Mostramos abaixo como ficam as equações (15) em função da letra
como angulo de rotação. Observe que limitamos 
ao intervalo 
.
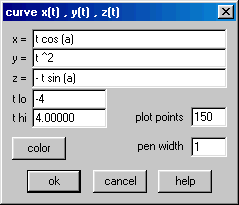
Ao variar o parâmetro com o mouse, você deverá ver algo parecido com a animação seguinte.