Numa atividade anterior com o Winplot estudamos o efeito de uma rotação de ângulo ![]() sobre o ponto
sobre o ponto ![]() . Variando
. Variando ![]() com o mouse, vimos o ponto em movimento circular em volta da origem. Seria interessante se pudéssemos fazer o oposto: fixar um valor para
com o mouse, vimos o ponto em movimento circular em volta da origem. Seria interessante se pudéssemos fazer o oposto: fixar um valor para ![]() e observar o efeito da rotação de ângulo
e observar o efeito da rotação de ângulo ![]() sobre um ponto variável no plano cartesiano.
sobre um ponto variável no plano cartesiano.
Considere, por exemplo, uma rotação de ![]() (isto é, tome
(isto é, tome ![]() ). Cada ponto
). Cada ponto ![]() é girado de
é girado de ![]() no sentido positivo, dando como resultado um novo ponto
no sentido positivo, dando como resultado um novo ponto ![]() . Seria interessante se pudéssemos movimentar o ponto
. Seria interessante se pudéssemos movimentar o ponto ![]() e, ao mesmo tempo, acompanhar a trajetória do ponto girado
e, ao mesmo tempo, acompanhar a trajetória do ponto girado ![]() . É intuitivamente claro que se, digamos, o ponto
. É intuitivamente claro que se, digamos, o ponto ![]() andar em linha reta, o ponto
andar em linha reta, o ponto ![]() descreverá uma reta girada de
descreverá uma reta girada de ![]() . Investigações desse tipo propiciam um entendimento mais acurado da ação de uma rotação sobre pontos do plano. Como visualizar essa variação simultânea?
. Investigações desse tipo propiciam um entendimento mais acurado da ação de uma rotação sobre pontos do plano. Como visualizar essa variação simultânea?
Embora não pareça, estamos lidando aqui essencialmente com um problema de gráficos de certas funções. Uma rotação no plano ![]() , tal como vimos estudando, define uma transformação de pontos do plano em si mesmo. Cada ponto
, tal como vimos estudando, define uma transformação de pontos do plano em si mesmo. Cada ponto ![]() é transformado pela rotação num ponto
é transformado pela rotação num ponto ![]() que depende do primeiro. Mas isto nada mais é do que uma instância do conceito de função.
que depende do primeiro. Mas isto nada mais é do que uma instância do conceito de função.
Cada rotação de ângulo ![]() define (ou é) uma função de
define (ou é) uma função de ![]() (o plano cartesiano) em
(o plano cartesiano) em ![]() . Na verdade, parte do que fizemos anteriormente consistiu em descobrir a “lei” que regula uma tal função. Como agora sabemos, uma rotação de angulo
. Na verdade, parte do que fizemos anteriormente consistiu em descobrir a “lei” que regula uma tal função. Como agora sabemos, uma rotação de angulo ![]() leva cada par
leva cada par ![]() no ponto
no ponto
![]()
Colocando isso em termos ainda mais explícitos: a rotação de ângulo ![]() é a função
é a função
![]()
definida por
![]()
Nosso problema no primeiro parágrafo dessa seção é este: fixado um ![]() , visualizar o gráfico da função
, visualizar o gráfico da função ![]() .
Estritamente falando, isto é impossível: o gráfico de
.
Estritamente falando, isto é impossível: o gráfico de ![]() é um conjunto de quádruplas ordenadas; se fossem duplas ou triplas,
poderíamos marcá-las no plano ou no espaço. Todavia, é possível
“enxergar” o comportamento de
é um conjunto de quádruplas ordenadas; se fossem duplas ou triplas,
poderíamos marcá-las no plano ou no espaço. Todavia, é possível
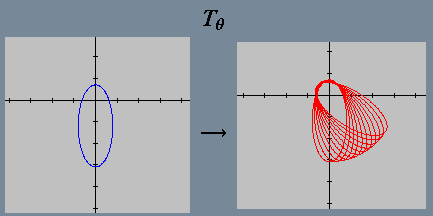
“enxergar” o comportamento de ![]() simplesmente colocando o seu domínio e a sua imagem lado a lado (conforme
ilustramos abaixo). Isto pode ser feito nas versões mais recentes do Winplot, conforme mostraremos em seguida.
simplesmente colocando o seu domínio e a sua imagem lado a lado (conforme
ilustramos abaixo). Isto pode ser feito nas versões mais recentes do Winplot, conforme mostraremos em seguida.