Clique no botão abaixo para iniciar uma pequena animação.
Os quadros desse filme foram feitos no Winplot aplicando-se rotações espaçadas de ângulos 
em volta do eixo 
à circunferência de centro 
e raio 1. As equações respectivas são mostradas abaixo.
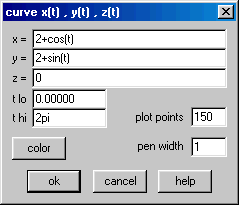
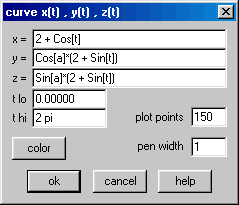
Considere os significados dos parâmetros 
e
. A variação de 
de
a 
gera sucessivamente um arco no plano 
que se fecha numa circunferência. A variação de 
gera uma “pilha” circular de circunferências em volta do eixo 
. Se fizermos
variar de maneira contínua, sem saltos, de a
, a pilha de circunferências dará uma volta completa e se transformará numa superfície em forma de pneu. Essa superfície 
que é muito apreciada pelos matemáticos 
é chamada toro.
Podemos afirmar que um toro é a superfície gerada pela rotação de uma circunferência ao redor de uma reta contida no plano da circunferência e que não a intercepta. Pelo fato de ser obtido revolvendo-se uma curva em torno de uma reta, o toro é um exemplo de superfície de revolução. A geratriz da superfície é a curva em rotação.
A discussão acima nos leva imediatamente à parametrização de superfícies. Como toda superfície de revolução, o toro pode ser descrito matematicamente em termos de equações paramétricas. Pelo que vimos há pouco, à medida que o ponto 
percorre o conjunto 
, as triplas ordenadas da forma 
varrem o espaço gerando o toro. Tradicionalmente, esta informação é apresentada escrevendo-se
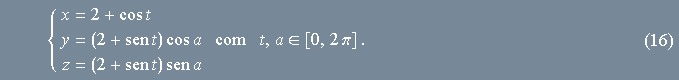
Estas são as equações paramétricas que definem o toro mostrado nas animações acima. Enquanto as equações paramétricas de curvas possuem apenas um parâmetro, as equações paramétricas de superfícies envolvem sempre dois parâmetros. Mas é crucial ressaltar que, em ambos os casos, as equações paramétricas não são únicas. Uma mesma figura pode ser parametrizada por equações diferentes.
Com o Winplot, é possível gerar gráficos de superfícies dadas por equações paramétricas. Para ver o toro completo no Winplot, clique no item x=f(t,u),... do menu Equa do ambiente 3D e preencha a caixa que se abre (intitulada surface) como segue:
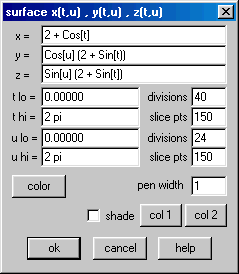
Conforme sugerimos acima, você pode aproveitar os dados da caixa curve
e copiá-los para a caixa surface. Observe, porém, um detalhe importante: substituímos a letra
por 
. Isto é absolutamente necessário no Winplot: os parâmetros de uma superfície
na caixa surface devem ser sempre 
e 
.
Do ponto de vista puramente matemático, a escolha das letras é irrelevante,
embora seja mais comum o emprego das letras “u” e “v”
como parâmetros de superfícies. (Esta é a convenção adotada no DPGraph.)
Com as facilidades de animação existentes em softwares como o Winplot e o DPGraph, você pode experimentar em tempo real o efeito de cada parâmetro sobre o gráfico de uma superfície. O fantástico grau de entendimento que se atinge desta maneira dificilmente pode ser alcançado pela mera observação de figuras em livros.