Acabamos de ver que a rotação de curvas é simples quando se utilizam equações paramétricas. Se a curva for dada por equações cartesianas, a questão se complica um pouco.
Vejamos o caso de uma curva 
definida implicitamente por 
. (Não nos cabe discutir aqui as restrições que 
deve cumprir para originar realmente uma “curva” no plano.) Dada uma transformação
, qual é a equação que define 
? Para o caso em que a função
é inversível (como acontece quando 
é uma rotação), tem-se a seguinte equação:
Exemplo 8
Para uma rotação 
, a função inversa é dada por
conforme se depreende da nossa discussão sobre matrizes de rotação. Deste modo, dada uma curva 
definida por uma equação do tipo
a equação cartesiana da curva após a rotação de ângulo 
será
Exemplo 9
Curvas dadas por equações da forma 
são um caso particular do Exemplo 8. Basta definir
Conseqüentemente, após girarmos uma curva 
de um ângulo 
, obteremos uma curva de equação
Exemplo 10
Vamos testar a equação (13) no Winplot. Comece abrindo a caixa de funções do usuário (menu Equa) e definindo uma função 
qualquer. Na figura abaixo, tomamos 
.
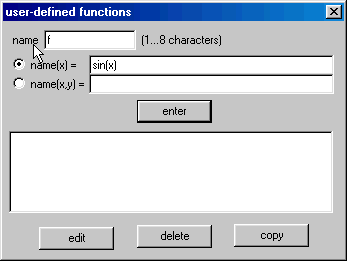
Clique no botão 
e feche a caixa. Em seguida, abra a caixa de funções implícitas e entre com a equação (13):
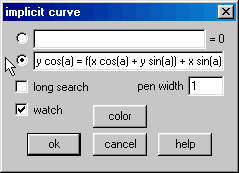
Repare que usamos “
” para o ângulo de rotação. Desmarque a opção watch (olhar) se quiser que o gráfico apareça de pronto. Agora, varie a constante 
. O gráfico da função seno começará a girar a cada clique nas setas, conforme ilustramos na
animação abaixo.
Você pode voltar à caixa de funções do usuário e modificar a definição de 
para ver a rotação de uma nova curva.