Vimos na página anterior como o mapeador do Winplot nos permite explorar, simultaneamente, uma curva 
no plano e a sua transformada 
por uma rotação 
. Entretanto, este recurso fantástico do Winplot possui uma limitação: a curva 
tem que ser traçada com o mouse. Por causa da imprecisão do traçado à mão livre, não podemos nos divertir com curvas matematicamente desenhadas na tela 
como uma parábola, por exemplo. Seria muito mais interessante e instrutivo se pudéssemos especificar uma curva por suas equações na janela domínio e ver a curva imagem na segunda janela.
Por exemplo, entrando com a equação 
na janela domínio da rotação 
, veríamos na janela imagem a parábola girada de 
. É possível que Richard Parris venha a implementar este recurso, mas não precisamos aguardar. O próprio Winplot nos permite apresentar as duas curvas num mesmo plano (em vez de em planos separados). Mais ainda: podemos fazer uma curva girar controlando matematicamente a sua equação, tal como já o fizemos com um ponto! Basta ensinar o Winplot a matemática necessária.
Nosso problema agora é:
|
Conhecida a equação de uma curva |
.
Ver-se-á que ganharemos muito mais em percepção se generalizarmos o problema para uma transformação qualquer 
, apesar de usarmos apenas as rotações como exemplo. A idéia geral é bem simples: o efeito de uma transformação
sobre uma curva
é o efeito resultante de
sobre cada ponto da curva. Na linguagem padrão da Matemática, podemos dizer que a curva transformada é simplesmente o conjunto-imagem 
da curva (conjunto)
pela transformação (função) . Nestes termos, o problema fica assim: dada a equação da curva
, determinar a equação da curva
.
Estritamente falando, a questão ainda não está bem colocada. Uma curva em
pode ser especificada por diversos tipos de equações: cartesianas, polares, paramétricas, etc. As equações paramétricas, embora pouco discutidas antes da universidade, são amiúde mais simples e flexíveis.
Exemplo 7
Vejamos o caso do arco da parábola
dado parametricamente pelas equações
Essas equações simplesmente especificam a forma de um ponto genérico do arco. Cada ponto do arco é da forma 
, onde
t é um número real no intervalo especificado. Aplicando a cada ponto do arco a rotação
, obtemos
Entre com essas expressões no Winplot conforme mostramos abaixo. Note-se que usamos “
” em vez de
“
” e, para maior destaque,
separamos os fatores de cada produto por um asterisco (embora isto não seja obrigatório no Winplot).
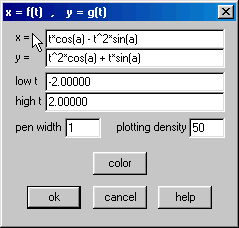
Agora, abra a caixa da constante 
e varie o parâmetro. Você verá a parábola girando em torno da origem. Clique no botão abaixo para ver uma pequena animação que ilustra o que dissemos. (Para reiniciar o filme, pressione a tecla F5.)
NOTA. Conforme foi observado ao final da página anterior, o mapeador do Winplot foi modificado em outubro de 2002. As modificações feitas por Richard Parris, a meu pedido, eliminam as limitações apontadas acima. O novo mapeador pode ser acessado logo na porta de entrada do Winplot, não mais pertencendo ao menu Misc.