Vejamos como estudar graficamente o comportamento de rotações no Winplot enxergando-as como funções 
.
Exemplo 6 (utilizando o mapeador)
Abra o arquivo Exemplo2 que criamos no Exemplo 2. No inventário temos o ponto
Este ponto é a imagem do ponto 
pela rotação 
(na notação da página anterior). O que fizemos no Exemplo 2 consistiu em examinar a ação sobre
de várias rotações, para diferentes valores de 
. Substituiremos agora o ponto
por um ponto genérico
. Com os recursos de cópia (Ctrl+C) e colagem de texto (Ctrl+V), podemos aproveitar as expressões acima para criar as seguintes:
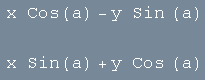
Clique no item 3-dim para entrar no ambiente tridimensional do Winplot. Abra o item z=f(x,y) do menu Equa e entre sucessivamente com as equações acima.
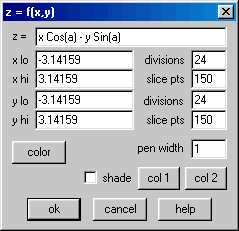
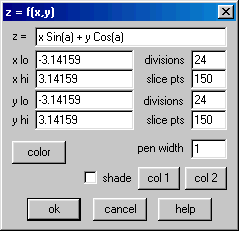
Cada clique em OK produz um gráfico de superfície. Contudo, não estamos interessados nos gráficos de 
e 
.
Não estamos interessados nessas funções de 
e 
pelas superfícies que produzem, e sim porque são componentes da rotação 
. Agora, ainda no ambiente 3D do Winplot, vá ao menu Misc
e clique no item Mappings... para abrir o mapeador do Winplot. Surgirão duas pequenas janelas intituladas domain (domínio) e range (imagem). Cada uma delas é uma cópia do
. Examine os menus de cada uma delas e configure-as como abaixo:
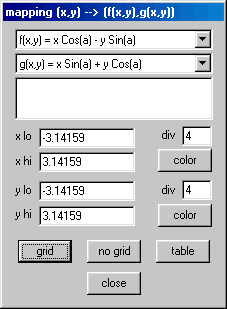
No menu Anim, fixe o valor de
em sessenta graus.
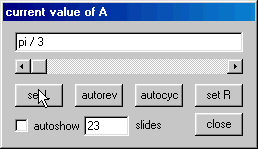
Volte às janelas domínio e imagem. Coloque o cursor sobre o domínio, pressione o botão esquerdo do mouse e arraste. O Winplot marca a trajetória do cursor na janela domínio e, simultaneamente, traça a curva transformada pela rotação na janela imagem.
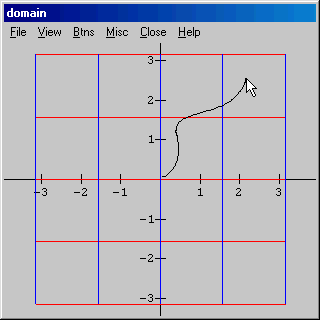
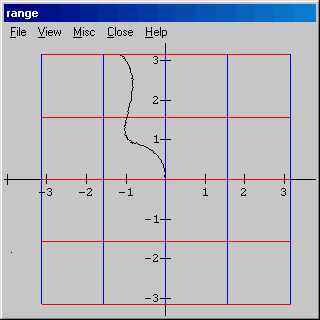
A curva imagem é a curva que você traçou girada de 
radianos (ou
) no sentido anti-horário.
Para apagar as curvas, clique em Erase drawing
(no menu Btns do domínio ou no menu View da janela imagem). Clique no item Cursor (menu Btns
) do domínio para substituir o traçado à mão livre por um ponto em cruz. A a imagem desse ponto pela função
aparecerá na segunda janela.
Com o mapeador do Winplot podemos estudar não somente rotações, mas transformações mais gerais do plano em si mesmo. Em particular, é possível visualizar funções 
, assunto que deixaremos para outra ocasião.
NOTA. Em 16 de outubro de 2002, o mapeador do Winplot foi totalmente reformulado, de modo que as instruções acima já não mais se aplicam à versão atual. Entretanto, o leitor não terá dificuldades em fazer as devidas adaptações.