Uma maneira de adquirir familiaridade com as equações de rotação
consiste em testá-las em casos simples, facilmente previsíveis sem as mesmas.
Exemplo 1
Se um ponto sobre o eixo 
sofre uma rotação anti-horária de 
, é evidente que ele cairá sobre o seu simétrico. Ora, um ponto genérico sobre o eixo 
tem a forma 
. O simétrico desse ponto em relação à origem é 
. Portanto, uma rotação positiva de 
leva o ponto
no ponto . Vejamos se esta conclusão pode ser obtida das equações de rotação. De acordo com essas equações, após uma rotação de ângulo 
, o ponto 
será transformado no ponto 
, onde
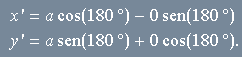
Como 
e 
, ficamos com 
e 
. Isto é, 
. O resultado confere!
Exemplos deste tipo são instrutivos e devem ser feitos manualmente sempre que possível. Mas este é um caso em que a experimentação tradicional torna-se rapidamente enfadonha e, pior, infactível. Mesmo para os poucos ângulos cujos senos e co-senos admitem expressão algébrica, os pontos girados podem ser difíceis de se localizar no plano. É nessas horas que se sente a falta de um “laboratório de Matemática” que permita experimentos rápidos, precisos e virtualmente ilimitados. O Winplot é um desses laboratórios.
Exemplo 2
Utilizando o Winplot, marque o ponto 
no plano cartesiano.
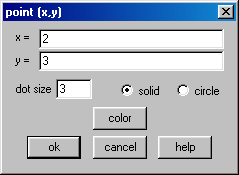
Utilizemos a letra 
para denotar ângulos.
De acordo com as equações (4), após uma rotação de ângulo
em volta da origem, o ponto
se deslocará para a posição
Entre com esse ponto no Winplot e salve o seu arquivo com o nome Exemplo2 para uso posterior. Recorde-se que se deve escrever “sin” (ou “Sin”, já que o Winplot não distingue maiúsculas de minúsculas) em vez de “sen”.
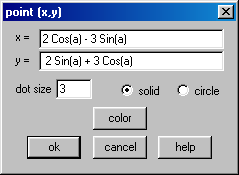
Após clicarmos em 
, continuaremos a ver apenas o ponto . Como sabemos, o Winplot inicia com 
, de modo que o novo ponto coincide com o
primeiro. Entretanto, se fizermos 
variar, crescendo a partir de 
, veremos o ponto
girar em torno da origem!
Bem, o que acontece “realmente” acima não é propriamente um movimento do ponto
ou do ponto 
. O ponto geométrico em si mesmo continua lá, estático. Mas imagine que cada ponto do plano possui uma pequena lâmpada sobre si. Para cada valor de 
, o Winplot acende a lâmpada sobre o ponto que se obtém de
por uma revolução de 
radianos em torno da origem. É o “piscar” das lâmpadas em diferentes posições que gera a impressão de um ponto móvel sobre a tela.
O que vemos na tela pode ser descrito como o movimento de um objeto a partir da posição de abscissa 2 e ordenada 3. Mas, matematicamente falando, não faz sentido dizer que o ponto
se move, embora venhamos a privilegiar essa forma “cinemática” de expressão. Além disso, esta é uma excelente oportunidade para se apreciar a relevância da Matemática na Física. As equações que estamos discutindo têm aplicações reais na Mecânica.
Exemplo 3
Em vez de acompanhar o movimento do ponto
com o mouse, podemos pedir ao Winplot para gerar um “rastro” do movimento utilizando a caixa abaixo:
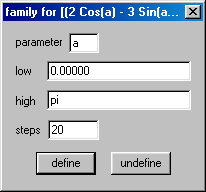
Aqui especificamos uma variação do parâmetro
de 
a 
(pi). Após clicarmos em
, veremos pontos igualmente espaçados sobre um arco de 
que começa em
.
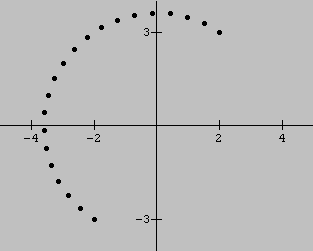
O raio desse arco é 
, a distância de
à origem.
Exemplo 4
Os exemplos anteriores são suficientes para nos convencer de que o ponto
se move sobre uma circunferência com a variação de . Se ainda tem dúvidas, então faça a circunferência aparecer! O raio, como vimos, é 
. A equação cartesiana da circunferência de raio
e centro na origem é
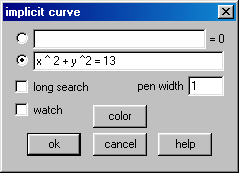
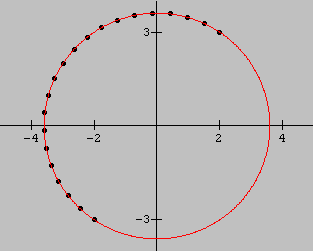
Entre com essa equação no Winplot e veja por si mesmo. (Aliás, essa equação já surge por padrão na caixa de equações implícitas do programa.)
Exemplo 5 (rotações negativas)
Até agora ilustramos rotações de ângulos positivos. Uma rotação negativa vai ao contrário, isto é, gira no sentido horário. Comprove isso no Winplot deslocando barra de rolagem do parâmetro
para a esquerda. Você verá o ponto
se mover no sentido dos ponteiros de um relógio.