Para obter a adjunta de uma matriz quadrada 
, primeiro formamos a matriz dos cofatores dos elementos 
de
.
Por definição, o cofator de
é o produto de 
pelo determinante da submatriz de
que se obtém removendo a linha e a coluna que passam por .
Formada a matriz dos cofatores, a sua transposta será a matriz adjunta.
Exemplo 1
Se
então a matriz dos cofatores é
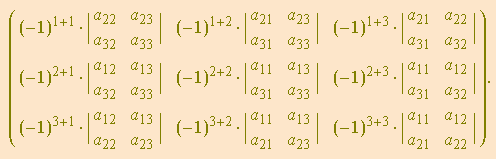
Transpondo a matriz dos cofatores, obtemos a adjunta de 
:
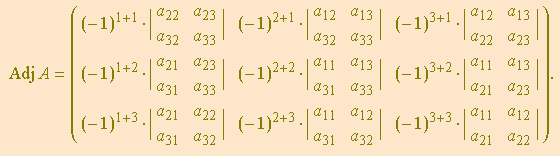
A idéia de formar uma “monstruosidade” como a adjunta surge naturalmente quando se toma conhecimento de dois resultados clássicos sobre determinantes:
“Teorema (elementar) de Laplace”. A soma dos produtos dos elementos de uma fila por seus respectivos cofatores é o determinante da matriz.
“Teorema de Cauchy”. A soma dos produtos dos elementos de uma fila pelos cofatores dos elementos de uma fila paralela é igual a zero.
Nestes enunciados, “fila” significa linha ou coluna.
Exemplo 2
Com relação à matriz
se formarmos a soma dos produtos dos elementos da primeira linha pelos seus respectivos cofatores, o resultado será o determinante:
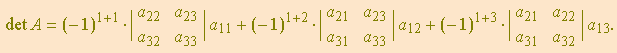
Isto vale para qualquer linha ou coluna, isto é, para qualquer fila. É o famoso “desenvolvimento por cofatores” de um determinante.
Exemplo 3
Por outro lado, a soma dos produtos dos elementos da primeira linha pelos cofatores dos elementos de outra linha é zero. Assim, multiplicando os elementos da linha 1 pelos cofatores dos elementos da linha 2 e somando os produtos, obtemos
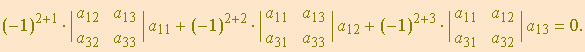
Os teoremas de Laplace e Cauchy podem ser fundidos numa única expressão, a saber:
|
Teorema. Se
|
, então
Aqui, 
é a matriz identidade de ordem 
.
Exercício 1
Utilizando (8), mostre que
.
Assim, uma matriz e a sua adjunta comutam: o produto de uma pela outra não depende da ordem.
Na próxima página mostraremos qual é a relevância da igualdade (8) para uma melhor compreensão da falsidade da condição (T2).