Uma aplicação importante do conceito de característica ocorre no teorema abaixo, tradicionalmente atribuído a Eugene Rouché (1832-1919) 
embora formulado diferentemente. Apresentaremos uma demonstração em outra oportunidade, numa seção deste site dedicada à Álgebra Linear. Neste último contexto, a sofisticação das técnicas torna o teorema relativamente fácil e a referência a Rouché desaparece por completo. Entretanto, devido ao caráter “elementar” da nossa exposição, preferimos manter a denominação consagrada em textos mais antigos. (Para aqueles que estejam cursando a disciplina Variáveis Complexas, informamos que não há conexão direta com o “Teorema de Rouché” sobre zeros de funções complexas.)
No enunciado abaixo, usamos as seguintes notações. O número de soluções do sistema linear
é indicado por 
, conforme já o fizemos antes. Lembramos que 
indica a característica da matriz 
. Finalmente, por 
indicamos a matriz aumentada de 
pela matriz 
. No caso abaixo,
é a matriz completa do sistema. Note-se que, sendo 
submatriz de
, vale 
.
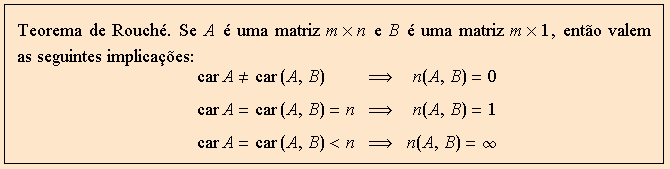
Estude atentamente as informações contidas nesse resultado. Observe como temos um critério relativamente simples. O sistema
é possível se e somente se a matriz dos coeficientes e a matriz completa têm a mesma característica. Se o sistema for possível, comparamos a característica com o número de incógnitas: se forem iguais, o sistema é determinado; do contrário, indeterminado. Isto encerra a questão!
Exemplo 7
Com base no Teorema de Rouché, podemos ver facilmente que a condição (T2) é verdadeira quando restrita a sistemas “homogêneos”. Mais precisamente, considere um sistema quadrado
em que 
. Um tal sistema tem pelo menos uma solução (a saber, 
), de modo que, pelo Teorema de Rouché, 
. Admitamos agora que vale a hipótese de (T2):
onde os 
são os determinantes 
da Regra de Cramer. Observe que a hipótese
já acarreta a nulidade dos determinantes 
(todos têm pelo menos uma coluna de zeros). Mas como 
, segue-se do
Exercício 3 que 
. Assim,
Uma nova aplicação do Teorema de Rouché nos dá 
, isto é, o sistema é indeterminado. Esta conclusão vale para todo sistema homogêneo cujo determinante é zero. Isto explica por que o exemplo considerado na
Introdução funciona.