Página extraída do Capítulo VII (Sistema de Numeração Posicional) do CD Números da coleção Matemática para Gregos & Troianos (edição revisada). O código HTML foi reprogramado para exibição neste site. Parte do conteúdo original foi omitida, mas o texto restante foi mantido intacto.
© Carlos César de Araújo, 3 de setembro de 2002
Considere um número natural qualquer, digamos
Observe que podemos reescrevê-lo assim:
ou assim:
ou ainda, assim:
Reconhece a forma desta expressão? O que temos aqui é algo como um polinômio do quinto grau. Podemos dizer que a igualdade
é verdadeira para
Quando nos
referimos a "
", estamos apenas usando
uma notação abreviativa para a expressão que realmente importa, a
saber,
É aqui que se
encontra a chave para o entendimento de muitas das propriedades dos
números que dependem dos seus algarismos. Todo número natural pode ser
escrito como um polinômio em 
cujos coeficientes
são os algarismos do número dado. Esses algarismos, por sua vez,
são apenas os números
As operações aritméticas básicas que
realizamos com os números são operações sobre certas formas polinomiais
com coeficientes restritos apenas ao conjunto 
. Esses polinômios podem
ser manipulados com o auxílio das regras do "cálculo algébrico" com as
quais estamos acostumados, mas com a restrição de que os polinômios
resultantes dessas operações tenham os seus coeficientes confinados ao
conjunto .
Um número de dois algarismos tem a forma geral
em que
e
Na prática, quando as letras 
e 
são números
específicos, escrevemos simplesmente
em vez de 
. Por exemplo, "
" é o mesmo
que
.
É como se tivéssemos um polinômio do
primeiro grau em 
e decidíssemos representá-lo por
,
mencionando apenas os seus coeficientes mas
deixando implícito que o primeiro coeficiente é o coeficiente de 
e que o segundo
coeficiente é o "termo constante". Os coeficientes desses polinômios,
porém, não podem ser números quaisquer; devem pertencer ao
conjunto
.
(CONTEÚDO ORIGINAL RETIRADO)
O uso de índices, como no Exemplo anterior, é um recurso de notação extremamente poderoso porque facilita o processo de generalização. Um número com n + 1 algarismos pode ser colocado sob a forma
na qual
e 
Se
substituirmos 
por uma letra, digamos
, a expressão
resultante
é, então, um polinômio de grau 
em 
com
coeficientes no conjunto .
Na vida diária, não lidamos propriamente com a expressão
mas com a notação abreviada que consiste em simplesmente escrever os coeficientes numa linha, uns ao lado dos outros, como
Ou seja, neste contexto,
Quando aprendemos esta notação pela primeira
vez, na infância, é claro que não temos condições de enxergá-la como
escondendo a expressão polinomial que é a sua essência. Dizem-nos apenas
que cada algarismo 
possui um
"valor absoluto"
e um
"valor relativo".
Na expressão geral acima, o "valor absoluto"
de 
é o
próprio 
, ao
passo que o seu "valor relativo" é 
. O valor relativo depende
da posição do algarismo, donde o emprego do termo "sistema
posicional".
Aprendemos também a dar nomes aos algarismos separando-os em colunas, como abaixo
e a fazer a leitura dos números pelo agrupamento dos algarismos em classes. Cada grupo de três algarismos, da direita para a esquerda, representa uma classe.
(CONTEÚDO ORIGINAL RETIRADO)
Suponhamos que você decidisse usar uma notação abreviada para polinômios que mencionasse apenas os coeficientes, começando com o da mais alta potência e incluindo zeros para os termos ausentes. Por exemplo, em vez de
você escreveria apenas
e em vez de escrever
você usaria
Então você rapidamente veria que pode operar com polinômios usando apenas esta notação. Por exemplo, a soma
seria escrita
Dispondo os cálculos como
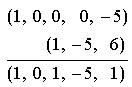
você percebe que a soma é obtida pela
simples adição dos coeficientes; não foi preciso mencionar a variável 
durante o
processo. Analogamente, você pode multiplicar polinômios empregando apenas
os seus coeficientes, sem usar a variável (embora, neste caso, seja
necessário mais cuidado e atenção).
A maneira como
operamos com os números por meio de suas representações decimais segue
exatamente a mesma idéia do último Exemplo: lidamos apenas com os coeficientes de um
polinômio numérico em 
. Há somente uma
diferença: os coeficientes resultantes não podem ultrapassar 
. Quando isto
acontece, substituímos o resultado pelo resto da divisão por 
e enviamos o
quociente para a coluna da esquerda.
Consideremos dois números 
e 
com
dois algarismos e procuremos entender o que se passa quando os
somamos da maneira usual. Para isto, escrevamos os números na forma
polinomial
onde 
e 
são os algarismos de
e
os de
.
Portanto, após agruparmos os termos semelhantes, teremos
Podemos afirmar que 
é um número com dois
algarismos? Isto só será verdade se pudermos garantir que 
e 
pertencem a
.
Como regra geral, nada mais podemos dizer. Contudo, é possível transformar
o polinômio
em outro que tenha a forma decimal. Para
isto, dividamos 
por 
e chamemos o quociente e
o resto de 
e 
, respectivamente. De
acordo com a igualdade fundamental da divisão, teremos
Portanto, após substituir e agrupar, vem
Observe que o quociente 
passou para a coluna das
dezenas. É precisamente isto que fazemos quando somamos os números. Quando
dispomos os número um sobre o outro
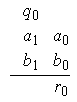
o número 
que fica é precisamente
o resto por 
da soma dos algarismos
e
; e o
número que "vai" é precisamente o quociente dessa soma por 
.
Analogamente, se dividirmos 
por 
, chamando o
quociente e o resto de 
e 
, teremos
donde, após nova substituição,
Nesta última expressão, estamos certos de que os números
pertencem a . Pois 
e 
foram
definidos como certos restos por 
, logo só podem assumir
os valores de 
a 
. (O que você diria sobre
?) A
disposição anterior fica agora assim:
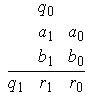
Por exemplo, na adição
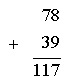
a soma dos algarismos 
e 
é 
. O resto de 
por 
é 
e o quociente
é 
.
Assim, escrevemos o resto 
debaixo do traço
vertical e transportamos o quociente 
para a coluna das
dezenas.
Analisemos a soma 
substituindo os numerais
pelos respectivos polinômios. Como
e
,
temos:
Podemos operar com esses polinômios em 
da mesma
maneira como o fazemos com polinômios numa variável 
. Assim, se agruparmos os
termos semelhantes, teremos
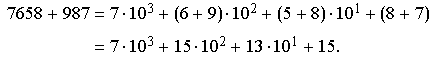
Contudo, não podemos enfileirar os
coeficientes do polinômio 
numa linha como,
digamos,
.
De acordo com as convenções do sistema
posicional, isto só pode ser feito quando os coeficientes são inferiores a
.
Contornamos facilmente o problema decompondo os coeficientes e
rearranjando a expressão resultante. Assim, notando que
obtemos
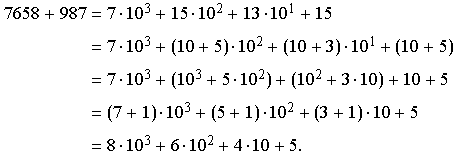
Agora, os coeficientes do polinômio 
são todos
menores do que 
, de modo que podem ser
concatenados como 
. Portanto,
.
Todo polinômio em 
pode ser reescrito de
forma que os seus coeficientes sejam algarismos decimais, isto é,
numerais que denotam números de zero até nove. Como exemplo,
considere
.
Efetuando a divisão por 
do último coeficiente e
escrevendo-o de acordo com a igualdade fundamental da divisão,
teremos:
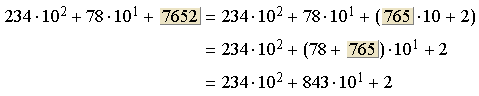
Repita o processo, dessa vez com 
:
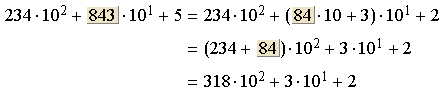
Façamos o mesmo com 
e assim por diante, até
obter coeficientes inferiores a 
:
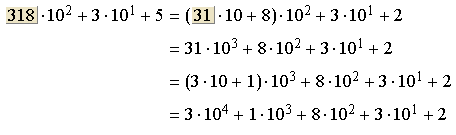
A transformação de
em
pode ser vista da seguinte maneira. Colocando os coeficientes em colunas separadas,
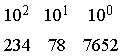
substitua cada coeficiente pelo seu
resto por 
e transporte o seu
quociente para a coluna da esquerda. O resultado final será:
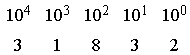
A maneira como normalmente efetuamos uma adição de numerais posicionais é essencialmente uma aplicação desse processo, exceto que, na prática, realizamos o transporte logo após a soma de uma coluna.
(CONTEÚDO ORIGINAL RETIRADO)
(BARRA DE NAVEGAÇÃO RETIRADA)
© Carlos César de Araújo, 3 de setembro de 2002