Problema Enviado
"Se um segmento 
tem 2 cm de comprimento, então a flecha do arco capaz de 
desse segmento mede:
(A) 
(B) 
(C) 
"
(Questão enviada por Dalton Vila Corte)
"Se um segmento tem 2 cm de comprimento, então a flecha do arco capaz de desse segmento mede:
(A)
(B)
(C) "
(Questão enviada por Dalton Vila Corte)
Para muitos, a principal dificuldade com este problema é o significado de “arco capaz de um ângulo” e de “flecha” de um arco. Clique no link abaixo para uma breve recordação desses conceitos.
Uma vez compreendida as definições dos termos relevantes, somos imediatamente levados a uma figura como a seguinte, na qual 
e, portanto, 
.
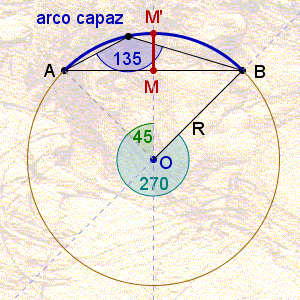
Nosso problema é o cálculo de MM´, o comprimento da flecha do arco capaz de 
sobre o segmento. Uma maneira de resolver a questão consiste em observar o triângulo retângulo 
e tomar o ângulo inscrito de vértice M´. Então
e daqui já tiramos o valor da flecha, desde que consigamos “expandir” o valor da tangente em termos de radicais (como sugerem as opções). Isto se consegue com as “fórmulas de divisão” da Trigonometria. Como os estudantes raramente se lembram de tais fórmulas, deixaremos este caminho como exercício.
Podemos tentar exprimir MM´ em termos de segmentos que sejam mais fáceis de calcular. A figura acima deixa claro que
,
onde R é o raio do arco capaz. Isto nos leva a descobrir pelo menos duas equações (igualdades) envolvendo R e OM. Observe que R e OM são lados do triângulo 
, retângulo em M. Da definição do cosseno, vemos que
ao passo que a definição do seno nos dá
Decorre da igualdade (ii) que 
. Substituindo esse valor em (i), vem 
. Portanto, o comprimento da flecha do arco é
.
No problema, conhecemos um cateto (MB) e um ângulo agudo (
) de um triângulo retângulo, o que é suficiente para a determinação dos demais elementos. De fato, este é um dos quatro casos clássicos da resolução de triângulos retângulos.
É altamente instrutivo examinar problemas simples como esse com um programa de Geometria Dinâmica. Neste mês, a seção Softwares começa a divulgar a versão Java do software C.a.R que, além de ser muito boa, é de graça! Com essa versão, é possível criar applets, pequenos aplicativos que permitem interação dinâmica com objetos geométricos pela Internet. (Applets com base em códigos do Mathematica já foram apresentados no site.) Clique no botão abaixo para abrir um applet numa janela independente que mostra a construção do arco capaz do ângulo de sobre um segmento a partir de um ângulo congruente adjacente ao segmento. (Dependendo da sua conexão, a primeira ativação do applet pode levar 3 minutos.)
O C.a.R, como quase todos os softwares da sua categoria, permite a realização de medidas (comprimentos, ângulos e áreas). O applet acima foi programado para exibir a medida da flecha com 5 casas decimais. (Se necessário, use o botão direito do mouse para mudar o valor de lugar.) O valor mostrado (
) coincide com a aproximação de 
com cinco decimais exatos. Como
é um número irracional, esta verificação numérica está longe de ser uma demonstração da correção da resposta, mas não deixa de ser um valioso indício. Seria bom que os softwares de Geometria Dinâmica fizessem cálculos simbólicos, mas ainda não estamos nesse estágio. Entretanto, a relevância desses softwares para o ensino da Geometria é incontestável e o seu impacto sobre a educação matemática tem sido assombroso.
Todas as ilustrações do problema foram feitas com o C.a.R.
Mostre que a flecha do arco capaz de um ângulo 
(
) sobre um segmento de comprimento 
mede
Mostre que
Carlos César de Araújo, 15 de abril de 2003