REVISÃO

Durante a breve exposição abaixo, tenha em mente que palavras como "segmento" e "ângulo" são ambíguas: ora se referem a uma figura geométrica, ora designam a medida da figura.

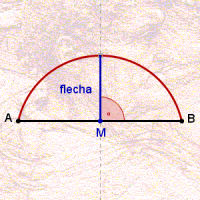
Seja um arco (de circunferência). A flecha de é o segmento que liga o ponto médio da corda ao ponto médio do arco. Alternativamente, se M é o ponto médio da corda, então a flecha do arco é o segmento , onde N é a interseção do arco com a perpendicular a por M.

Agora, considere um ângulo com vértice no arco e lados passando pelos extremos do arco. Dizemos que esse ângulo é inscrito no arco. Um resultado fundamental sobre "ângulos notáveis" na circunferência é que todos os ângulos inscritos em um arco são congruentes.

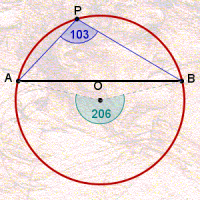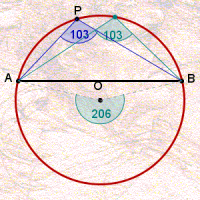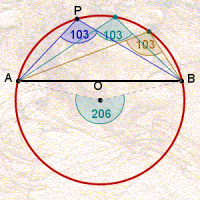
 A medida comum desses ângulos vale a metade do ângulo central associado ao arco. A animação abaixo ilustra essa relação para diferentes arcos numa mesma circunferência.

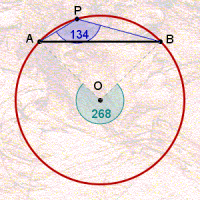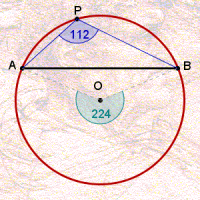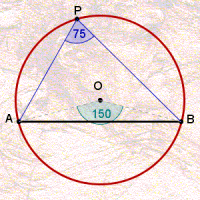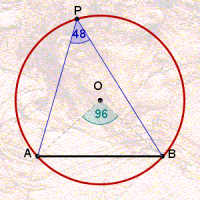
Portanto, todo arco determina um ângulo , qual seja, a medida que é comum a todos os seus ângulos inscritos.

O conceito de "arco capaz" surge quando invertemos as coisas: dados um segmento e um ângulo , podemos perguntar pelo arco cujos ângulos inscritos medem . Dizemos que é "o" arco capaz de no segmento . Qualquer arco cujos ângulos inscritos medem é um arco capaz de .

Exemplo

Podemos dizer que "o" arco capaz "do" ângulo reto é "a" semicircunferência. Isto é uma maneira "inversa" (e sucinta) de dizer que todos os ângulos inscritos numa semicircunferência medem .