Problema
“Determine o lugar geométrico dos centros das circunferências tangentes simultaneamente às duas circunferências descritas pelas equações
![]() e
e ![]() .
.
Obs: considere todos os casos possíveis.”
“Determine o lugar geométrico dos centros das circunferências tangentes simultaneamente às duas circunferências descritas pelas equações
![]() e
e ![]() .
.
Obs: considere todos os casos possíveis.”
Recordemos que as posições entre duas circunferências podem ser descritas em função da distância entre os seus centros. (Se quiser interromper as animações abaixo num determinado quadro, pressione a tecla Esc. A tecla F5 rebobina o filme.)
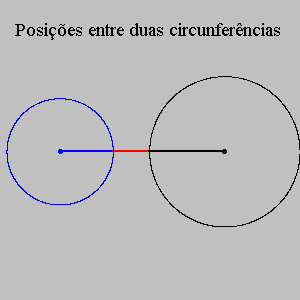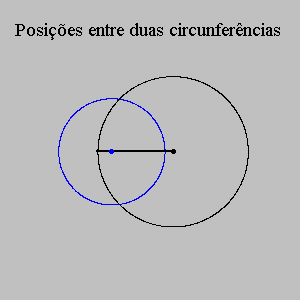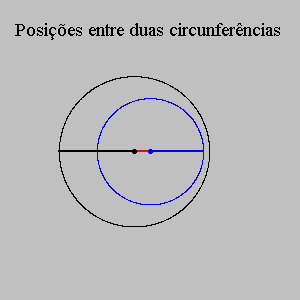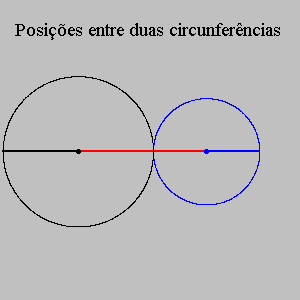
O quadro abaixo resume três situações simples, bem conhecidas e relevantes para o nosso problema.
| posições | distância entre os centros | |
|---|---|---|
| internas | menor que | diferença dos raios |
| tangentes internamente | igual a | diferença dos raios |
| tangentes externamente | igual a | soma dos raios |
Para utilizar essas informações, precisamos conhecer os centros e os raios das duas circunferências dadas. Comparando coeficientes ou completando quadrados, verifica-se facilmente que a equação ![]() pode ser escrita como
pode ser escrita como
![]() .
.
Trata-se, pois, da circunferência com centro em ![]() e raio 4. Analogamente, como a equação da segunda circunferência é
e raio 4. Analogamente, como a equação da segunda circunferência é
![]() ,
,
seu centro é ![]() e seu raio é 1. A distância entre esses centros é 2, que é menor que
e seu raio é 1. A distância entre esses centros é 2, que é menor que ![]() . Portanto,
. Portanto,
a circunferência ![]() está no interior de
está no interior de ![]() .
.
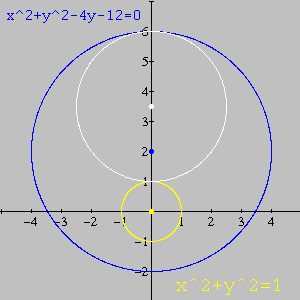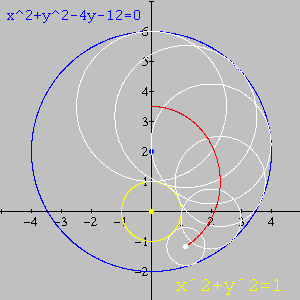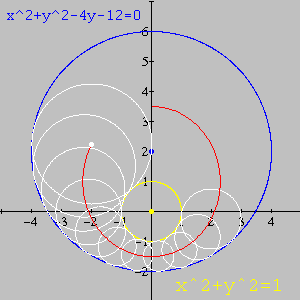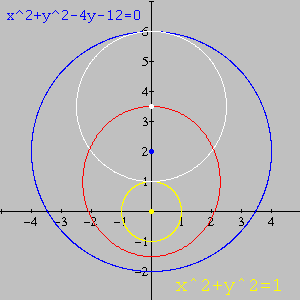
É óbvio que se pode tirar esta conclusão após um simples desenho a mão livre (usando o polegar como a ponta seca de um compasso). A figura abaixo foi feita no Winplot.
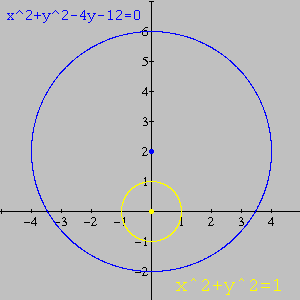
Agora, seja C uma circunferência tangente às duas acima. Chamemos o seu raio de r. É evidente que C não pode tangenciar externamente a circunferência maior, donde r < 4. Isto nos deixa com apenas duas possibilidades, das quais discutiremos o caso mais óbvio em que C tangencia internamente a circunferência maior e externamente a menor. Então

Queremos o “lugar geométrico” dos centros de C. Isto significa: que conjunto é formado pelos centros de todas as circunferências C no caso considerado? Ora, adicionando as duas igualdades acima obtemos
distância do centro de C a ![]() + distância do centro de C a
+ distância do centro de C a ![]() = 5
= 5
Vemos que a soma das distâncias do centro de C a dois pontos fixos é constante (igual a 5), condição que caracteriza uma elipse. Esta elipse é o "lugar dos centros" de C.
A animação abaixo foi feita no Winplot com base nas conclusões acima. Além de confirmar a veracidade da resposta, ilustra dinamicamente o significado do problema.
Com base na nossa discussão, deduza as equações necessárias para montar uma animação semelhante no Winplot. (Atividades como essa originam novos desafios e exigem muito mais dos seus conhecimentos, mas as recompensas intelectuais são garantidas.)
A frase “o lugar geométrico dos centros de C é uma elipse” afirma uma certa igualdade entre dois conjuntos de pontos. No argumento acima, significa que a elipse é o conjunto dos centros de todas as circunferências C tangentes a ![]() e
e ![]() (para o caso considerado). Mas, rigorosamente falando, nosso argumento provou apenas que um conjunto contém o outro.
Que inclusão foi provada? Como você provaria a inclusão contrária? (Este exercício serve para mostrar que a definição precisa de "lugar geométrico dos centros de C " não é tão simples como se esperaria — uma sutileza lógica comumente ignorada quando se discute problemas de "lugares".)
(para o caso considerado). Mas, rigorosamente falando, nosso argumento provou apenas que um conjunto contém o outro.
Que inclusão foi provada? Como você provaria a inclusão contrária? (Este exercício serve para mostrar que a definição precisa de "lugar geométrico dos centros de C " não é tão simples como se esperaria — uma sutileza lógica comumente ignorada quando se discute problemas de "lugares".)
O problema pede que sejam examinados “todos os casos possíveis”. Que casos seriam esses? Para o caso que ficou faltando, qual é o lugar geométrico? Clique no botão abaixo para ter uma idéia.
Carlos César de Araújo, 2 de fevereiro de 2003