Solução (por Carlos César de Araújo).

Discussão preliminar

Devido ao contraste entre “maior” e “menor”, o significado da frase “o maior inteiro menor ou igual a x” pode não se revelar claramente num primeiro contato. (Compare com o Problema Resolvido 8 desta seção.) Uma formulação gramaticalmente superior seria

“o maior inteiro que é menor ou igual a x”.

Ou seja, o piso de x é o maior inteiro que satisfaz a propriedade de ser menor ou igual a x. Uma formulação ainda melhor resulta da observação de que o conjunto dos inteiros que são menores ou iguais a x é . Então,

,

onde “max” significa “o maior elemento de”. Por igual modo,

,

onde “min” significa “o menor elemento de”. Embora nem todo conjunto de números reais tenha máximo ou mínimo, é intuitivamente óbvio que tem máximo. (Aliás, pode-se provar que isto é equivalente ao axioma de indução em . Veja a seção Lógica Matemática.)

Exercício 1

Mostre que a definição de é equivalente à seguinte afirmação:

é o número tal que .

Análise das opções

Examinemos cada uma das cinco afirmações da questão.

(001) afirma que se , então . Correto. Pois suponha que x é um inteiro. Então os inteiros são , dos quais o menor é o próprio x. Portanto, . Analogamente, os inteiros são , dos quais o maior é x. Isto mostra que . Essas duas conclusões nos dão .

(004) é falsa. De acordo com a definição inicial de piso, é o maior inteiro n para o qual . Dito de outro modo, é o maior inteiro n tal que . Uns poucos cálculos mostram que . Segue-se que .

(0016) é falsa. Pois , logo . Assim, o conjunto dos inteiros maiores ou iguais a é , e o menor elemento desse conjunto é . Portanto, .

Exercício 2

Vimos acima que se , então . Mostre que vale a recíproca: se , então .

Investigando com o computador

Todos os softwares divulgados neste site dispõem das funções piso e teto, cujas denominações em inglês são floor e ceiling, respectivamente. No Winplot, por exemplo, obtemos o gráfico de entrando com a expressão floor(x) na caixa de equações explícitas. (No gráfico abaixo, os extremos abertos e fechados dos segmentos foram criados como duas famílias de pontos.)

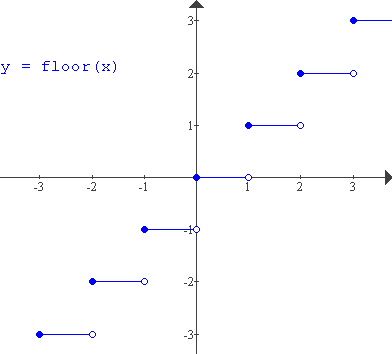
Para o gráfico de , deve-se digitar ceil(x). (Essa abreviação de ceiling é também usada no GrafEq, mas não no DPGraph e no Mathematica. Note-se que ceiling é um substantivo derivado do verbo ceil.)

Considerações finais

Conforme mostramos nos capítulos XIX e XX do CD Números, as funções piso e teto são formidavelmente úteis, e mereceriam um lugar de destaque já no ensino médio. Parabenizamos a UFMS pela excelente apresentação dessas funções numa prova de vestibular. Mas discordamos dos autores da questão quando afirmam que as notações de Iverson facilitam a compreensão dessas funções.

Até a década de 1960, o “maior inteiro menor ou igual a x” era comumente denotado por (lê-se “colchete de x”) e identificado com a “parte inteira de x”. Por volta de 1957, o canadense Kenneth E. Iverson (1920-), então na Universidade de Harvard, desenvolveu uma escrita simbólica para a expressão concisa de conceitos matemáticos, da qual emergiram as notações e . Tomadas em conjunto, elas realçam a dualidade das definições de piso e teto (uma se obtém da outra pela substituição dos termos “maior” e “menor” por “menor” e “maior”, respectivamente). Outra vantagem é que os semicolchetes não padecem da ambigüidade dos colchetes tradicionais da notação mais antiga, conforme discutimos no CD Números. Todavia, é evidente que a mera substituição de "" por "" em nada altera a complexidade intrínseca do conceito “o maior inteiro menor ou igual a x”.

Iverson apresentou sua escrita simbólica no livro A Programming Language, que ele publicou em 1962. Dois anos depois, suas idéias — incluindo o próprio título do livro! — foram utilizadas pela IBM no desenvolvimento de uma linguagem de programação de altíssimo nível chamada APL. Talvez interesse aos leitores deste site saber que vários aspectos da APL influenciaram Stephen Wolfram quando da criação do Mathematica, conforme, aliás, foi (discretamente) admitido por Wolfram no prefácio do seu recente e polêmico livro A New Kind of Science.