Solução (por Carlos César de Araújo)

Discussão preliminar

O problema acima é um clássico, mas para que sua análise seja instrutiva é preciso, antes de tudo, se convencer de que o argumento proposto é falacioso — mesmo sem perceber onde reside a falácia. (Veja o Exercício 2, abaixo.)

A igualdade é o exemplo mais importante de relação (binária) reflexiva, simétrica e transitiva. Os significados desses três termos são recordados abaixo (onde 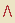é o sinal lógico para o conectivo “e”):

Reflexividade: .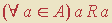

Simetria: .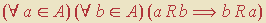

Transitividade: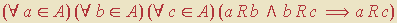

Exemplo 1

No conjunto 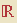dos números reais, a relação 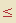(menor ou igual) é reflexiva e transitiva, mas não é simétrica.

Exercício 1

Encontre uma relação que seja reflexiva e simétrica, mas que não seja transitiva.

Exercício 2

Dê um exemplo de relação que seja simétrica e transitiva sem ser reflexiva.

Descobrindo a falha

As propriedades reflexiva, simétrica e transitiva são logicamente independentes: nenhuma implica outra, e duas delas não acarretam a terceira. Isto se prova mediante contra-exemplos apropriados. Em particular (Exercício 2), simetria e transitividade não garantem reflexividade. Então, onde reside a falha do argumento apresentado no problema?

Para facilitar a análise, vamos separar e enumerar os passos do argumento:

1. Considere um elemento a do conjunto A;
2. Tome um tal que 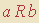(i.e., tal que a está na relação R com b);
3. Segue-se da simetria de R e do passo 2 que ;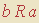
4. Segue-se da transitividade de R e dos passos 2 e 3 que .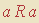
5. Decorre dos passos 1 e 4 que 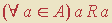, ou seja, R é reflexiva.

OBSERVAÇÃO

Agora, fica fácil descobrir uma dificuldade com o passo 2: de onde vem b? Como temos certeza de que podemos considerar um elemento tal que 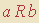? Afinal, é perfeitamente possível que o elemento a escolhido no passo 1 não mantenha a relação R com nenhum elemento de A.

Exercício 3

No conjunto dos números naturais, considere a relação R definida por “a é primo e b é primo”. Verifique que R é simétrica e transitiva. Em seguida, aplique o argumento acima a R, começando com 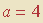no passo 1. Consegue ver que o raciocínio se “emperra” no passo 2? O argumento nos permite inferir que 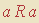quando a é 4?

Uma análise mais profunda

O problema em discussão ilustra um erro muito comum em demonstrações: a introdução despercebida de hipóteses. No caso acima, o autor do argumento introduziu, sub-repticiamente, a premissa de que existe um b tal que 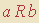. O Exercício 3 mostra que essa suposição existencial não pode ser garantida, em geral.

Algumas pessoas se embaraçam quando tentam uma formalização mais estrita do argumento. Por um lado, nossa análise pode ser resumida dizendo-se que o argumento não prova que 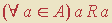, e sim que

para uma R simétrica e transitiva. Por outro lado, em vez de interpretar o passo 2 como supondo a existência de um b, podemos admitir que b foi dado condicionalmente: simplesmente tomamos um b qualquer tal que 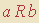— assim como tomamos um a qualquer no passo 1 sem nos comprometermos em supor . De acordo com esta segunda análise, os quatro primeiros passos do argumento provam que, para uma R simétrica e transitiva,

Bem, as duas análises são corretas! A dúvida é que elas parecem distintas: como em 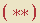só temos quantificadores universais, onde foi parar a hipótese de existência que teria sido introduzida às ocultas no passo 2? A resposta vem da “álgebra” dos quantificadores que rege o Cálculo de Predicados (um dos temas da seção Lógica Matemática deste site).

O fato é que as sentenças e 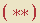são logicamente equivalentes! Nos termos da Lógica, é permitido passar de

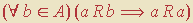
— uma quantificação universal de uma implicação — para

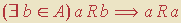
— uma implicação cujo antecedente é uma quantificação existencial —, e vice-versa; e isto porque a variável “b” não ocorre no conseqüente (isto é, “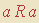” não depende de b). Um matemático “tradicional” poderia ver tudo de outro modo, pois raramente se preocupa em manipular quantificadores explicitamente. Ele freqüentemente o faz num nível “acima”, em termos de interseções, uniões e inclusões de conjuntos. Mas, em essência, tudo depende dos quantificadores.

Investigando com o computador

Na seção Laboratórios apresentaremos um artigo no qual mostramos como estudar relações binárias com o Mathematica. A idéia consiste em tratar relações binárias como conjuntos de pares ordenados (como, aliás, já se tornou comum na matemática), o que permite a busca automática de contra-exemplos para várias afirmações sobre relações finitas. Os leitores interessados em antecipações podem consultar os trabalhos de Klaus Sutner e Dana Scott, referenciados na página do Mathematica neste site (seçcão Softwares).