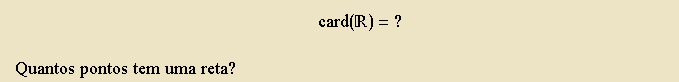
Um Salto Quântico No Infinito
Carlos César de Araújo
Artigo publicado no Jornal Estado de Minas em 4 de abril de 1998, na seção Pensar (então sob a direção de Ângelo Oswaldo, atual Secretário de Estado da Cultura de Minas Gerais). Salvo pequenas alterações estilísticas e a inclusão dos links e figuras, o texto abaixo reproduz o original.
Num provocante artigo escrito para esta seção ("Deus e o diabo na física quântica", 20/10/97), o físico e filósofo Armando Lopes de Oliveira discorre sobre as revoluções causadas pela Teoria da Relatividade e a Física Quântica, e afirma que esta última conduziu ao "mais desconcertante cenário epistemológico do século XX". Desejo riscar o "mais" e alargar o campo de batalha discutindo uma terceira revolução científica que ocorreu não só paralelamente às duas citadas, mas que tomou forma no interior de uma ciência (ou será uma arte?) que tem a reputação popular de ser a "mais certa" de todas e onde a razão supostamente impera inabalável: a Matemática.
Vamos começar pensando um pouco: quantos pontos tem uma reta? Como? Vença o susto inicial e lembre-se de que uma reta é formada de pontos — não é isto que nos ensinam na escola? Certo, certo ... Mas são pontos demais, uma infinidade. Como é possível contar uma coleção infinita? Aliás, faz sentido distinguir um infinito do outro? E o que é o infinito? Existem mesmo coleções infinitas? Você pode encarnar o espírito de Aristóteles e ir adiante. Por exemplo, a reta é a imagem arquetípica da continuidade; não exibe saltos ou buracos. Um ponto, por sua vez, é uma entidade discreta e isolada; talvez seja uma mônada, um átomo ou um infinitésimo. Como pode um contínuo ser formado de grãos indivisíveis?
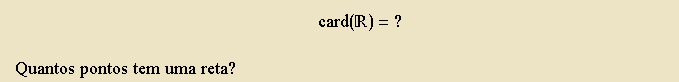
Questões como essas atravessaram os tempos atordoando gigantes do pensamento como Leibniz e Kant (que responderão "não" à maioria delas), mas só foram depuradas do misticismo, cientificamente esclarecidas e completamente resolvidas (acredita-se) no último terço do século XIX com a revolucionária teoria dos conjuntos, concebida e desenvolvida por Bolzano, Dedekind e, principalmente, Georg Cantor. A grande realização de Cantor foi a elaboração da primeira teoria matematicamente fecunda daquilo que Aristóteles chamou de "infinito atual" — uma multidão interminável de coisas pensadas como simultaneamente reunidas e coexistentes. Aparentemente desconhecido nas civilizações antigas do Egito, Mesopotâmia e Índia, esse infinito par excellence causou estardalhaço e trauma no pensamento grego através dos "paradoxos de Zenão". Por esse motivo (e outros), Aristóteles achou que era necessário disciplinar o raciocínio. Assim, inventou a Lógica e fez do infinito um tabu. Tradições às favas, Cantor ousou discernir, comparar e hierarquizar os infinitos. Tornando explícita e matematicamente manipulável a atividade imemorial de "contar", ele estendeu-a aos conjuntos infinitos, viu que nem todos são iguais, e que um infinito pode ser menor do que outro. Como os números 1, 2, 3, ... só permitem a contagem de coleções finitas, ele criou um novo tipo de número transfinito e pretendeu catalogar todos os conjuntos infinitos e atribuir-lhes um tamanho em termos desses novos números.
Dois tipos de infinito foram importantes no trabalho de Cantor. O primeiro é a base da sua hierarquia, o infinito enumerável, característico dos conjuntos cujos elementos podem ser colocados lado a lado com os números 1, 2, 3, ... simultaneamente. O segundo é o infinito do contínuo, próprio de conjuntos como a reta (a reta infinita das aulas de Geometria). Cantor descobriu que o infinito do contínuo é maior do que o infinito enumerável — um resultado que possui conseqüências matemáticas de longo alcance. No ambiente dessa teoria, a nossa questão inicial ("Quantos pontos tem uma reta?") torna-se: que lugar ocupa o contínuo na hierarquia de Cantor? Resposta: o segundo, logo após o enumerável. Mas isto foi um artigo de fé para Cantor até os seus últimos dias. Na verdade, ele nunca conseguiu provar que não pode haver um infinito intermediário entre esses dois, de modo que o seu palpite entrou para a história como a Hipótese do Contínuo. Apesar desse fracasso momentâneo, a introdução do conceito abstrato de conjunto e o estudo dos conjuntos infinitos constituíram uma das maiores conquistas intelectuais do século XIX. A tensão constante entre a aritmética e a geometria, entre o discreto e o contínuo, gerada pela primeira crise na Matemática (a descoberta dos números irracionais pela escola de Pitágoras), rompera-se pela primeira vez, mergulhada num esquema racional único que permitiu sintetizar um "contínuo aritmético" decente e solucionar os paradoxos de Zenão sem pressupor os antigos e problemáticos infinitésimos — assim como a Teoria da Relatividade fundiu a eletricidade e o magnetismo e explicou as ondas de Maxwell sem o fantasma do éter.
Nenhuma revolução é pacífica. Cantor encontrou opositores ferrenhos e até mesmo hostis. Seu arquiinimigo intelectual, Leopold Kronecker, rejeitou filosoficamente a introdução de entidades transfinitas na Matemática argumentando que "Deus criou os inteiros; o resto é obra do homem". Pode ser que Deus tenha se sentido tocado pela mão do homem quando Cantor mordeu o fruto proibido do infinito, mas, de qualquer modo, o castigo não tardou. Pelo fim do século XIX, enquanto alguns matemáticos começavam a apreciar, aplicar e estender as idéias de Cantor, outros ... descobriam contradições! O próprio Cantor descobriu (1895) que não poderia existir algo como o conjunto de todos os conjuntos: tal existência contradizia um fato básico provado por ele mesmo, segundo o qual não há um infinito maior do que todos os outros. Investigando a anomalia da existência de coleções que recusavam-se a existir, Bertrand Russell encontrou (1901) um paradoxo ainda mais assombroso nos fundamentos da própria Lógica, destruindo por completo o atraente programa de Dedekind-Frege-Peano (mostrar que toda a Matemática pode ser construída partindo de princípios "puramente" lógicos aplicados a conjuntos). Este foi o início da "crise dos fundamentos" da Matemática do século XX.
Ao mesmo tempo em que os físicos se debruçavam sobre os paradoxos que conduziriam à Relatividade e ao salto quântico de Planck, lógicos e matemáticos se empenhavam em eliminar os paradoxos da teoria dos conjuntos e preservar a parte saudável que se mostrara absolutamente indispensável. As opiniões se dividiram. Para alguns, já não era mais possível visualizar os conjuntos à maneira "ingênua" de Cantor; se se quisesse mantê-los na Matemática, ter-se-ia que tratá-los como entidades aceitas sem definição, mas, em contrapartida, regidas por axiomas, condições que restringissem o seu comportamento e que seriam aceitas sem sombra de dúvidas, com base apenas na sua fecundidade dedutiva. Para outros, o problema reclamava uma investigação mais apurada dos métodos sagrados de demonstração. Sob a pressão das circunstâncias, Ernst Zermelo propôs, em 1908, a primeira axiomatização da teoria dos conjuntos. Os axiomas de Zermelo conseguiam realmente evitar os "conjuntos paradoxais" então conhecidos. Mas como garantir que não haveria outros? Como seria possível assegurar de maneira absolutamente clara e sem ambigüidades que a Lógica e os axiomas não levariam a novas contradições?
Bem, vejamos. Para um físico, o resultado de um experimento só é aceito se for passível de reprodução. Para um matemático, uma demonstração só é aceita se for passível de verificação. Infelizmente, o ato de "verificar" pode ser subjetivo, algo dependente da mente daquele que verifica. Como evitar essa subjetividade? Verificação mecânica! Esta foi a base do plano derradeiro de David Hilbert. Hoje diríamos: verificação por computador. Hilbert sabia (como outros antes dele) que seria possível (essencialmente) programar um computador digital idealizado para imprimir teoremas ao ser alimentado com um banco de axiomas como os de Zermelo. O passo seguinte seria empreender um estudo matemático dessa máquina a fim de provar cabalmente a sua consistência, isto é, que ela não poderia jamais imprimir contradições. Uma tal máquina justificaria a matemática nela contida. Mas atenção: a matemática a ser usada numa tal prova de consistência não pode ser mais passível de dúvida do que aquela incorporada na própria máquina. Assim, Hilbert viu-se obrigado a provar a consistência da máquina por métodos programáveis nela mesma. Um belo plano. Por volta de 1928, o formalismo de Hilbert tinha colhido alguns sucessos parciais, suficientes para inflar-lhe o orgulho: "A matemática é uma ciência sem pressuposições. Para fundamentá-la, não preciso de Deus, como Kronecker." Hilbert esperava salvar o "paraíso" de Cantor.
Mas a razão tem razões que a própria razão desconhece. A década de 1930 marca um ponto de inflexão na história dos fundamentos da Matemática com a publicação dos teoremas de incompletude de Gödel-Rosser. Tome uma máquina pretensiosa como a de Hilbert e suponha que ela é consistente. O trabalho de Gödel mostra, em primeiro lugar, que é possível programar a máquina para gerar um enunciado indecidível, uma afirmação que foge à capacidade da máquina de poder comprová-la. Além disso, é possível gerar um enunciado indecidível que traduz a consistência da própria máquina, mostrando que, portanto, é impossível programar a máquina para provar a sua própria consistência — e com isso a matemática nela embutida. Esses dois resultados sepultaram definitivamente as ambições originais do logicismo de Russsell e do formalismo de Hilbert. "Deus existe porque a matemática é consistente, mas o Diabo também, porque não podemos provar este fato." Assim se pronunciou um matemático de uma influente escola francesa "neoformalista" chamada Bourbaki — a qual, misteriosamente, ignorou os teoremas de Gödel por mais de uma década após a sua publicação.
Percebeu-se logo uma analogia interessante entre os teoremas de Gödel e o princípio de incerteza de Heisenberg. Com efeito, ambos revelam limitações imprevistas na quantidade de informação que pode ser obtida quando se procura refinar duas atividades básicas e complementares: observação (na Física) e demonstração (na Matemática). E assim como Heisenberg não quis estabelecer nenhuma relação entre a incerteza quântica e o problema do livre-arbítrio, Gödel também não admitiu que as limitações da mecanização da Matemática (reveladas pelo seu teorema) pudessem refletir limites dos "poderes da razão humana". (Uma questão que seria debatida por Alan Turing. Mas trata-se de outra história ...)
Restava, contudo, uma esperança: as afirmações indecidíveis do trabalho de Gödel eram algo artificiais. Eram de truques de codificação numérica que não traduziam nenhum problema matemático importante, como a Hipótese do Contínuo, por exemplo — a qual, diga-se de passagem, Gödel acreditava ser falsa. Entretanto, a praga da indecidibilidade estava a caminho: em 1963 Paul Cohen mostrou que a Hipótese do Contínuo é indecidível! Para apreciar o impacto dessa nova descoberta, é preciso ressaltar que já pela metade do século XIX, cientes de uma geometria não-euclidiana (a de Lobachevsky) e de uma álgebra não-comutativa (os quatérnios de Hamilton), muitos matemáticos começaram a sustentar que a Matemática não diz respeito a coisa alguma e que seria legítimo investigar relações puramente esquemáticas entre entidades abstratas, sujeitas apenas ao requisito da consistência lógica. Acontece que a nossa cognição tem uma necessidade básica que é difícil de evitar: a necessidade de realidades às quais possamos nos referir — um impulso que acaba por criar realidades na mente. Assim, os matemáticos do século XX começaram a se apoiar num universo platônico de conjuntos como uma forma de atingir a realidade matemática última, na qual todas as coisas são conjuntos, nada mais que conjuntos. O método utilizado por Cohen (que lhe valeu a Medalha Fields em 1966) mostrou, porém, que essa "realidade" sofre de uma indeterminação aguda. Não apenas a Hipótese do Contínuo, mas uma pletora de outras questões matemáticas longamente não respondidas mostraram-se simplesmente irrespondíveis dentro de um quadro de intuições que pareciam seguras. As implicações epistemológicas e mesmo ontológicas ainda aguardam maiores esclarecimentos. Por exemplo, ao contrário da sentença de Gödel, a indecidibilidade da Hipótese do Contínuo não nos dá a menor indicação quanto à sua verdade ou falsidade.
Os físicos têm conseguido explicar os interstícios do átomo ao preço de nos fazer acreditar que a realidade é esquizofrênica. De forma semelhante, ao investigarem os supostos "átomos" da Matemática — os conjuntos —, os matemáticos tatearam uma realidade não menos louca, mas intelectualmente recompensadora. Basta dizer que foram os esforços iniciais de Frege, Russell, Hilbert e Gödel que assentaram os fundamentos teóricos da Ciencia da Computação, muito antes do surgimento do primeiro computador digital eletrônico. Mas a metáfora espacial por meio da qual enxergamos um conjunto como uma "caixa de objetos" tornou-se tão frágil e imprecisa quanto o modelo planetário do átomo. Já não se pode mais falar em "a" teoria dos conjuntos, pois conhecem-se agora diversas "teorias de conjuntos", diversos modelos alternativos para o conceito de contínuo, e com eles infinitas respostas para esta questão básica: quantos pontos tem uma reta? Há até mesmo outras abordagens fundamentistas rivais, não baseadas no conceito de conjunto. Aparentemente, tudo o que foi alguma vez imaginado pode agora ser pensado consistentemente. Por exemplo, os antigos infinitésimos, eliminados da Matemática com os trabalhos de Weierstrass e Cantor, foram parcialmente revividos pela análise não-convencional e completamente revividos (segundo alguns) nos "contínuos autênticos" da geometria diferencial sintética. Pior, dispomos agora de tantas "lógicas" que talvez não se possa mais dizer que haja mesmo uma única "razão". O historiador Morris Kline chegou a declarar a "perda da certeza". Alguns buscaram alento na neurologia, como o matemático A. R. D. Mathias, para quem as dificuldades de quantificar o contínuo se devem ao fato de as percepções analíticas e visuais se processarem em partes diferentes do cérebro. O estudo dos computadores tem forçado a adoção de novas atitudes. Numa frase: a situação está como o Diabo gosta! Sinal dos tempos? Bem, os matemáticos prosseguem contentes em seu trajeto pois, para a Ciência, o pior problema é o conjunto dos problemas tornar-se vazio. Kasparov perdeu para Deep Blue, é verdade ... Mas Andrew Wiles demonstrou o último teorema de Fermat.