
Curso POSCOMP
Estudar para o POSCOMP significa basicamente retomar uma gama de tópicos de toda uma graduação em Ciência da Computação. Daí a importância de se iniciar uma preparação sistemática a pelo menos um ano da prova. Exemplificando, considerando-se apenas o que o edital dispõe sobre Álgebra Linear, tem-se material suficiente para um período universitário. As partes de Teoria dos Grafos, Recursão, Cálculo e Autômatos também apresentam conteúdo considerável.
Em seu modelo atual, o curso cobre os seguintes conteúdos:
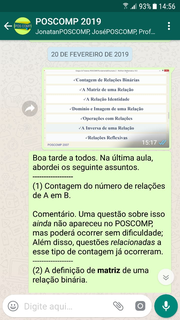
(1) o programa completo da prova de Matemática;
(2) as áreas matemáticas e lógicas da prova “Fundamentos da Computação” (como algoritmos, autômatos, linguagens formais, medidas assintóticas de complexidade e Teoria dos Grafos);
(3) as áreas matemáticas e lógicas da prova “Tecnologia da Computação” (como álgebra relacional e transformações geométricas).
Ao longo do curso os alunos recebem cadernos eletrônicos contendo as questões do POSCOMP devidamente classificadas em tópicos e complementadas com centenas de problemas extras que fornecem as definições, algoritmos e teoremas fundamentais, exemplos e ilustrações, discussões e técnicas básicas que estão envolvidos nas resoluções.
Carlos César de Araújo
NOVO: após cada aula POSCOMP, resumos e material adicional pelo WhatsApp.
 |
 |
 |
 |
 |
 |
Mostramos a seguir os principais cadernos do curso e seus respectivos conteúdos. Para alguns cadernos os tópicos não se encontram definidos de modo geral, pois a seleção dos mesmos é feita em conformidade com a experiência matemática de cada grupo.
Caderno 1: Lógica Matemática
• Parte I. Identificação de Padrões • Reconhecimento de Padrões (I)
• Parte II. Proposições e Sentenças Abertas • O conceito de Proposição • Proposições Singulares e Relacionais • Proposições com Quantificadores • Recíproca de “Todo A é B” • Proposições Compostas • Sentenças Abertas
• Parte III. Negação de Proposições • *Oposições • Negação • Dupla Negação • Negação de Desigualdades • Negação de “Todo A é B” • Negação de “Algum A é B” • O Quantificador “Nenhum”
• Parte IV. Os Operadores Lógicos Fundamentais • Conjunção (∧) • Disjunção (∨) • Lógica e Linguística: • Escopo da Negação • Leis de De Morgan
• Parte V. Proposições Condicionais • Condicional (material) • Lógica e Linguagem • A Tabela-Verdade do Condicional • Se • Recíproca do Condicional • Contrapositiva • Negação de Condicionais
• Parte VI. Formas Normais • Forma Normal Disjuntiva • Leis Distributivas • Identidades Lógicas • Construção de Formas Normais
• Parte VII. Proposições Bicondicionais • Somente se • Bicondicional • Negação de Bicondicionais • Necessidade e Suficiência
• Parte VIII: Cálculo de Predicados • Os Quantificadores ∀ e ∃ • Generalização das Leis de De Morgan • Quantificação Múltipla • Contagem Booleana
• Parte IX. Verdades e Falsidades Lógicas • Tautologias • Contradições e Contingências • Aplicações aos Fundamentos da Computação
• Parte X: Validade, Inferência e Dedução • Caracterizações de Validade • Argumento Correto • Dedução vs Indução • Silogismo (transitividade de ⇒) • Modus Ponens e Modus Tollens • Teorema da Dedução (introdução de ⇒) • Redução ao Absurdo • Verificação de Validade
• Parte XI: Metalógica
• Completude Funcional-Veritativa • Consistência, Completude e Decidibilidade
O Papel da Lógica neste Curso
O estudo da Matemática envolve três atividades fundamentais:
• definir.
• calcular.
• demonstrar.
Para a maioria das pessoas, a Matemática se confunde com a atividade de calcular, geralmente vista apenas como o emprego de regras de transformação sobre números e expressões simbólicas. Nesse sentido, “calculamos” quando efetuamos uma divisão, resolvemos uma equação, avaliamos um determinante, escalonamos uma matriz ou obtemos o valor de uma integral indefinida.
Todavia, a excelência matemática requer mais do que cálculos baseados em regras. À medida que avançamos, temos que lidar com teorias e abstrações cada vez mais potentes. Torna-se indispensável entender os conceitos e estabelecer relações entre os fatos fundamentais. O entendimento dos conceitos se faz por meio de suas definições. Os fatos fundamentais são axiomas e teoremas, os quais se relacionam entre si por deduções ou demonstrações. Tão importante quanto calcular é saber verificar se uma definição é acertada ou constatar se uma demonstração pode ser obtida a partir de certas premissas.
Definições e teoremas têm em comum o fato de serem proposições. O entendimento de uma definição e a compreensão de um teorema dependem da estrutura interna das proposições correspondentes. Essa estrutura pode ser explicitada por meio de uma linguagem simbólica que permite ver com mais facilidade o significado de uma proposição ou a correção de uma demonstração. O estudo das proposições e da arte de demonstrar é feito na Lógica.
A Lógica nos ensina como “dissecar” proposições e realizar demonstrações. Demonstrações podem ser feitas de maneira tão sistemática (algorítmica) quanto a execução de um cálculo. Além de sua importância no desenvolvimento de teorias, a habilidade com demonstrações tem também o efeito pedagógico de reduzir substancialmente o número de fatos a serem memorizados; pois então torna-se mais fácil e rápido deduzir um resultado do que decorá-lo e aplicá-lo sem entendimento. Além disso, todo cálculo pode ser reduzido a uma demonstração, a saber, a demonstração da proposição que afirma o resultado do cálculo. Demonstrar é uma atividade de importância suprema não só na Matemática, mas em todas as ciências, particularmente na Ciência da Computação.
Muitas questões das provas do POSCOMP envolvem demonstrações rápidas de proposições a partir de outras mais básicas (definições, axiomas ou teoremas). Portanto, o domínio da Lógica é fundamental para um bom desempenho neste exame.
Caderno 2: Conjuntos, Funções, Relações e Estruturas Algébricas
• Parte I: Linguagem Fundamental da Matemática
• O Conceito de Conjunto • Operações com Conjuntos • Produtos Cartesianos Finitos • Relações Binárias • Tipos Básicos de Relações • Composição de Relações • Funções • Partições de Conjuntos • Relações de Equivalência • Relações de Ordem • Aplicações aos Fundamentos da Computação
• Parte II: O Corpo dos Números Reais
• Propriedades de R • Desigualdades • Intervalos em R • Elementos Máximo e Mínimo de um Conjunto • Racionais e Irracionais
• Parte III: Funções Reais de Variável Real
• Funções e Gráficos • Retas • Função Módulo • Funções Definidas por Partes • As Funções Piso e Teto • Transformações em Gráficos
• Parte IV:
Equações e Funções do 2° Grau • Equação e Problemas do 2º Grau • Função do 2º grau • Inequações do 2º Grau • Máximos e Mínimos
• Parte V: Exponenciais e Logaritmos • Equações Exponenciais • Função Exponencial • Logaritmos • Exame de Questões Anuladas
• Parte VI • Definições de Demonstrações por Recursão • O Cálculo Lambda • Operadores quer Ligam Variáveis • Abstração Lambda • Reduções e Conversões • O Teorema de Curch-Rosser • O Cálculo Lambda com Tipos • Combinadores • Programação Funcional
Caderno 3: Combinatória
• Parte I: Cardinais, Conjuntos Infinitos e Enumeráveis • Cardinais • Conjuntos Enumeráveis
• Parte II: Métodos Básicos de Contagem Finita • Enumerações Elementares • Inclusão-Exclusão (2 conjuntos) • Ordem e Repetição • Princípio Fundamental da Contagem • Colorações
• Parte III: Somação Finita • Somatórios e Produtórios • PA e PG • Soma de PA • Soma de PG
• Parte IV: Agrupamentos sem Repetição • Arranjos • Permutações • Permutações Circulares
• Parte V: Agrupamentos sem Repetição (Combinações) • Combinações Simples • Uso de Complementação • Problemas Envolvendo Partições
• Parte VI: Coeficientes Binomiais • Binômio de Newton • Conjunto Potência • Coeficientes Binomiais
• Parte VII: Agrupamentos com Repetição • Arranjos com Repetição • Combinações com Repetição • Coeficientes Multinomiais:Permutações com Elementos Repetidos • Problemas Variados
• Parte VIII: Mais Métodos de Contagem • Inclusão-Exclusão (3 conjuntos) • O Princípio das Gavetas • O Princípio das Gavetas (II) • Inclusão-Exclusão (caso geral) • Parte XIX: Contagens Especiais • Contagem de Relações • Contagem de Funções • Contagem de Partições • Exame de Questões Anuladas
Caderno 4: Cálculo de Uma Variável
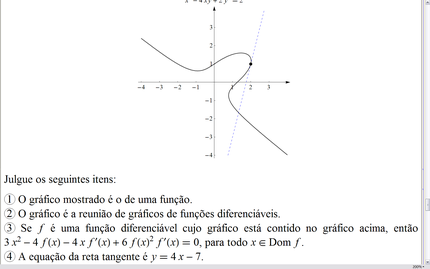
• Parte I: Limites • Noções Métricas e Topológicas Básicas • O Conceito de Limite • Cálculo de Limites • Assíntotas
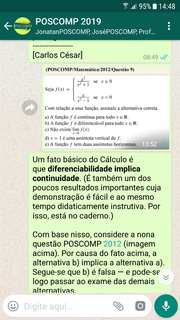
• Parte II: Funções Contínuas • Continuidade
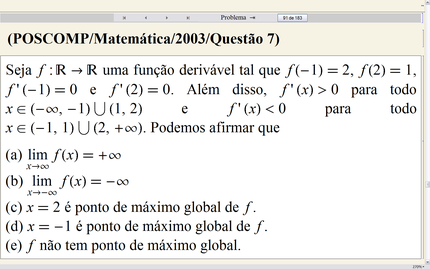
• Parte III: Cálculo Diferencial • Cálculo Básico de Derivadas • A Regra da Cadeia • Derivadas de Funções Inversas • Significado Geométrico da Derivada • Taxas de Variação • Propriedades da Derivada • Máximos e Mínimos • Convexidade • Indeterminações e Regra de l’Hôpital
• Parte IV: Cálculo Integral • Integração Indefinida • O Primeiro Teorema Fundamental do Cálculo • O Segundo Teorema Fundamental do Cálculo: Integração Definida por Primitivação • A Integral Definida como Área • Funções Pares e Ímpares • Aproximações da Integral • Propriedades da Integral Definida • Integrais Impróprias • Volumes por Integração
• Parte V: Séries • Séries • Testes de Convergência • Séries de Taylor
• Parte VI: Tópicos Suplementares • Exame de Questões Erradas ou Anuladas
 |
 |
 |
 |
 |
 |
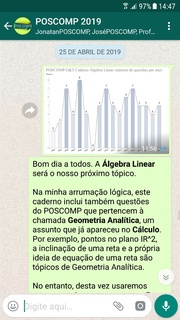
Caderno 5: Álgebra Linear e Cálculo de Várias Variáveis
• Parte I: Números Complexos • Operações Básicas • Representação Polar
• Parte II: Álgebra Matricial • Matrizes • Adição e Produto por Escalar • Multiplicação de Matrizes • Transposta • Traço • Escalonamento • Posto • Determinante • Matriz Inversa • Matrizes Ortogonais • Matrizes Idempotentes
• Parte III: Espaços Vetoriais • Axiomas de Espaço Vetorial • Combinação Linear • Subespaços • Soma de Conjuntos • Dependência Linear • Base e Dimensão • Somas Diretas
• Parte IV: Transformações Lineares • Transformações Lineares • Núcleo e Imagem • O Teorema do Posto • Operadores Polinomiais
• Parte V: Variedades Lineares (subespaços afins) • Equações Paramétricas • Retas
• Parte VI: Equações Lineares • O Princípio da Superposição • Classificação de um Sistema Linear
• Parte VII: Espaços com Produto Interno • Formas Bilineares • Norma e Distância • Ortogonalidade • Produto Vetorial • Planos e Hiperplanos
• Parte VIII: Teoria Espectral • Autovalores e Autovetores • O Teorema de Cayley-Hamilton • Diagonalização • Geometria Analítica • Áreas e Volumes • Transformações Geométricas • Quádricas • Aplicações aos Fundamentos da Computação
• Parte IX: Cálculo de Várias Variáveis • Sistemas Não Lineares • Derivadas Parciais • Gradiente • Otimização
 |
 |
 |
 |
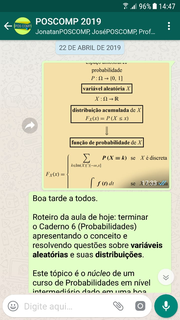
Caderno 6: Probabilidades
• Parte I: Fundamentos • Espaço Amostral de um Experimento • Definição de Probabilidade • Princípio de Inclusão-Exclusão
• Parte II: Probabilidades e Combinatória • Probabilidades e Combinatória
• Parte III: Eventos Condicionados e Independentes • Probabilidade Condicional • Independência
• Parte IV: Funções de Variáveis Aleatórias • Valor Esperado e Variância
• Parte V: Modelos Probabilísticos Especiais • Distribuição Hipergeométrica • Binomial e Poisson • Distribuição Geométrica
Caderno 7: Estística
Conteúdo personalizado.
Caderno 8: Iteração, Recursão e Análise de Algoritmos
• Parte I: Análise Assintótica • As Notações Ο, ο, Ω, ω e Θ • Aplicações ao Cálculo • Aplicações aos Fundamentos da Computação
• Parte II: Recursão • Funções Recursivas • Equações de Recorrência
• Parte III: Iteração • Pontos Fixos de Funções • Aproximações Sucessivas • Aplicações aos Fundamentos da Computação • Aplicações: Contagem de Strings Binárias • Recursão Múltipla
 |
 |
Caderno 9: Teoria dos Números
Conteúdo personalizado.
Caderno 10: Grafos
• Grafos • Conexidade • Colorações • Grafos Eulerianos • Grafos Hamiltonianos • Grafos Planares • Árvores • Grafos Isomorfos • Complemento de um Grafo • Representações de Grafos
Caderno 11: Autômatos e Linguagens Formais
Conteúdo personalizado.
Carlos César de Araújo